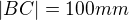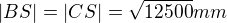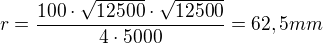Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 04. 2012 18:04
Poloměr kružnice
Zdravím. Počítám Františka Bělouna a zasekl jsem se u tohoto příkladu. Vůbec netuším, jak to vypočítat. Asi bych si tam udělal nějaký trojúhelník, ale nevím kde.
Je dán čtverec 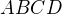 s délkou strany
s délkou strany 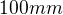 . Vypočítejte poloměr kružnice, která prochází vrcholy
. Vypočítejte poloměr kružnice, která prochází vrcholy 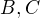 a středem strany
a středem strany 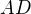
Quidquid latine dictum sit, altum videtur - Cokoli je řečeno latinsky, vypadá vznešeně.
Offline
#2 14. 04. 2012 18:33
Re: Poloměr kružnice
↑ Janisek: pokud je bod  středem strany
středem strany 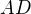 , tak se snažíme vypočítat kružnici opsanou trojúhelníku
, tak se snažíme vypočítat kružnici opsanou trojúhelníku  , střed této kružnice leží v průsečíku os stran trojúhelníku
, střed této kružnice leží v průsečíku os stran trojúhelníku 
pro velikost poloměru  kružnice opsané, platí
kružnice opsané, platí 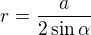
když si ten trojúhelník překreslíš tak, aby jsi ho měl na výšku, označíš  (je rovnoramenný), tak
(je rovnoramenný), tak 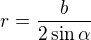 kde
kde  je úhel při vrcholu
je úhel při vrcholu 
neměl by být problém jakýmkoliv způsobem určit ten úhel, dokážeš si totiž vypočítat strany trojúhelníka
Offline
#4 14. 04. 2012 19:06
#6 14. 04. 2012 19:11
#8 14. 04. 2012 22:44
#10 15. 04. 2012 18:02
#11 15. 04. 2012 19:39
Re: Poloměr kružnice
Prvně jsem počítal přes Pythagorovu větu 


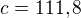 takže poloměr vyjde děleno dvěma to vyšlo těch
takže poloměr vyjde děleno dvěma to vyšlo těch  . A pak jsem počítal podle tvého vzorečku
. A pak jsem počítal podle tvého vzorečku 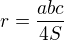 a to mi vyšlo, že
a to mi vyšlo, že 
 A k těm 70,71 jsem se dostal tak, že
A k těm 70,71 jsem se dostal tak, že 
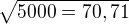
Quidquid latine dictum sit, altum videtur - Cokoli je řečeno latinsky, vypadá vznešeně.
Offline
#12 15. 04. 2012 20:00
Re: Poloměr kružnice
↑ Janisek: k tomu prvnímu - střed kružnice opsané není ve středu strany  , ale leží na výšce trojúhelníku
, ale leží na výšce trojúhelníku 
k tomu druhému - strany trojúhelníka nejsou 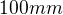 ale
ale 
rozklikni si skrytou část v předchozím mém příspěvku
Offline
#14 15. 04. 2012 20:15
Re: Poloměr kružnice
↑ Janisek: jo promiň, jsem o příspěvek pozadu :) hlavní je, abys to pochopil (i své chyby)
Offline
#15 15. 04. 2012 20:41
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Poloměr kružnice
↑ Janisek:
Šlo by to počítat i takto:
Využívám analytickou geometrii
Nikdo není dokonalý
Offline