Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Struktura izomorfní s vesmírem (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 02. 2012 22:46
- Sokolik
- Příspěvky: 27
Struktura izomorfní s vesmírem
Co myslíte, že můžeme říct o matematický struktuře izomorfní s vesmírem (nebo prostě o jeho matematickém modelu)? :)
Vycházejme z toho, že za "logické univerzum" naší struktury vezmu časoprostor. Čili logickým individuem je tu bod/element časoprostoru.
Málokdo by popřel, že vesmírný prostor je kontinuum. (Určitě se dá i nějak dokázat, že dělení prostoru na elementy neodpovídá realitě, ale to snad není třeba.)
Víc lidí říká, že je konečný. Neomezený, ale konečný. To je ale buď blud, nebo tito lidé nemluví o "celkovým vesmíru". Kdyby byl prostor zacyklen ve vyšším rozměru (jako povrch míče je zacyklen do třetího rozměru), tak je vesmír vícerozměrný. Potom musíme uvažovat tento vícerozměrný prostor. Ten je zase buď nekonečný, nebo konečný a zacyklen do vyššího rozměru. atd., v celkovým součtu mi vychází, že časoprostor (aťsi má kolik rozměrů chce) je nutně nekonečný.
I když ohledně mohutnosti jeho univerza to kupodivu nehraje roli, protože je kontinuum.
Počítám, že jeho mohutnost zůstává stejná, i kdyby měl třeba nekonečně rozměrů.
Jak můžeme definovat jeho individua, čili body (časo)prostoru? Asi jim musíme přiznat nějakou hodnotu, abychom pak mohli říkat, že vůbec něco existuje. Vychází mi, že můžeme zůstat na hodnotách 0/1 a pořád to bude izomorfní se strukturou, která udílí jakejkoli větší počet hodnot (včetně mohutnosti kontinua?)
Univerzum vesmíru mi vyšlo jako kontinuum nul a jedniček. Co si o tom myslíte? Jsem spíš syntetik než analytik, takže potřebuju kontrolu a vyhledávám debatu.
Offline
- (téma jako vyřešené označil(a) Sokolik)
#2 08. 02. 2012 08:08
Re: Struktura izomorfní s vesmírem
↑ Sokolik: Pekne pozdravujem a pripájam názor iba k jednému pojmu z Tvojho príspevku.KONTINUUM. Pomenovanie kontinuum pri súčasných poznatkoch o mikrosvete, by sme mali používať veľmi opatrne, už aj s ohľadom na kvantový charakter častíc a interakcií častíc aj s elmg. žiarením.
Môže to (kontinuum) ale aj byť vytvorené v ľudskej fantázii a tam prosím sa medze nekladú.
Offline
#3 08. 02. 2012 17:55 — Editoval Sokolik (08. 02. 2012 17:59)
- Sokolik
- Příspěvky: 27
Re: Struktura izomorfní s vesmírem
↑ pietro:
Taky zdravím,
tos teda zareagoval na něco, co jsem nejmíň čekal. Kdyby časoprostor nebyl kontinuum, mělo by to hodně zvláštní filozofický důsledky, který tu nechci na matematickým fóru rozebírat.
V moderní fyzice se celkem přiznává, že TEORIE SE TVOŘÍ TAK, ABY ODPOVÍDALY PRAXI. I kvantový pojetí energie vzniklo tímhle způsobem. Ani není žádnej jinej způsob, jak ověřit pravdivost teorie o přírodním zákonu, než že bude odpovídat starým i novým empirickým poznatkům. Fyzika si nemůže klást nároky na poznání absolutních zákonů, protože ona jen vysvětluje souhrn konkrétních pozorování. Proto se v metafyzických otázkách vůbec nemusíme cítit omezeni poznatky z fyziky, protože ta slouží zcela jiným účelům a musela by překročit vlastní stín. Jinak řečeno, FYZIKY SE TOHLE VŮBEC NETÝKÁ
Kromě toho, kvantová fyzika neříká, pokud vím, nic o kvantování časoprostoru.
Spíš mě zajímalo, JESTLI NENAJDETE NĚJAKOU CHYBU V MÝCH DEDUKCÍCH OHLEDNĚ MOHUTNOSTI ČASOPROSTORU (řekněme za předpokladu, že se opravdu jedná v zásadě o kontinuum, čili úsečku můžu neustále dělit a nikdy nenarazím na "metafyzickou hranici").
(Mám v předchozím příspěvku nepřesnost, chtěl jsem říct, že počítám, že existuje izomorfismus mezi strukturou, která každýmu bodu kontinua udělí 0/1, a strukturou, která mu udělí i jakýkoli vyšší číslo, ať už celý, nebo reálný.)
Hodně zvláštní mi přijde například to, že MOHUTNOST ZŮSTANE STEJNÁ, AŤ MÁ VESMÍR KONEČNOU, NEBO NEKONEČNOU VELIKOST. V praxi by to mělo znamenat, že tyhle dvě alternativy nelze od sebe rozlišit. Přitom je zřejmý, že je rozlišit lze...(?)
Offline
#4 11. 02. 2012 21:38
- Sokolik
- Příspěvky: 27
Re: Struktura izomorfní s vesmírem
Je zvláštní, že mi nikdo nechce nebo nemůže odpovědět ani na čistě matematickou část mý otázky...
"Dvouhodnotová" struktura vesmíru vlastně znamená, že mohutnost možných vesmírů je 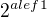 , což je totéž jako pro 3hodnotovou (
, což je totéž jako pro 3hodnotovou ( ) atd. Takže mám pravdu :)
) atd. Takže mám pravdu :)
Jen mi furt vrtá hlavou, jak je možný, že konečně velkej vesmír je, coby kontinuum, stejně mohutnej jako nekonečně velkej. Určitě by k tomu mohla něco říct matematická topologie...
Offline
#5 30. 03. 2012 12:03 — Editoval Rumburak (30. 03. 2012 15:13)
Re: Struktura izomorfní s vesmírem
↑ Sokolik:
Ahoj.
Nemohu se ku Tvým tématům vyjadřovat příliš fundovaně, protože filosofií vesmíru se nezabývám.
Navíc se domnívám, že vztah mezi matematikou a filosofií není o vzájemném prolínání, ale o dvou zcela různých přístupech k věci.
Uvedu jeden dotaz:
V jakém (matematickém ?) významu chápeš termín KONTINUUM ?
A jednu poznámku:
Funkce tangens zobrazuje vzájemně jednoznačně inteval 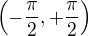 na interval
na interval  , takže oba tyto intervaly
, takže oba tyto intervaly
mají tutéž mohutnost (a sice tzv. mohutnost kontinua), přestože první je omezený a druhý neomezený.
Offline
#6 16. 04. 2012 01:22 — Editoval Sokolik (16. 04. 2012 01:25)
- Sokolik
- Příspěvky: 27
Re: Struktura izomorfní s vesmírem
↑ Rumburak:
Ahoj Rumburáči.
Termín kontinuum chápu přesně tak, jak ho chápeš ty. Čili třeba jako množinu o mohutnosti reálných čísel. (Z toho fyzikálně-filozofickýho hlediska je důležitá vlastnost hustoty. Protože jako hustej je vesmír obvykle chápán.)
Je mi známo, že kontinuum lze zobrazit bijekcí na svou vlastní část, o tom přece právě píšu. Připadá mi, že z matematickýho hlediska je tedy VESMÍR (jakožto kontinuum) STEJNĚ VELIKEJ JAKO TŘEBA JABKO. Což ovšem evidentně není pravda. Už jen ten výraz, "věc je stejně mohutná jako její část", naznačuje jakousi odtrženost od reality. Ptám se, KDE SE VZAL TEN PARADOX A JAK HO VYŘEŠIT.
Pohled mimo matematiku, na skutečnej svět, tak jako tak potřebujeme, abysme mohli kontrolovat, jestli nám matika neříká úplný bludy, neshodující se s evidencí. A zdali jsou to bludy, to řešíme pomocí filozofie :)
Offline
#7 16. 04. 2012 11:45 — Editoval Rumburak (16. 04. 2012 14:58)
Re: Struktura izomorfní s vesmírem
↑ Sokolik:
Ahoj Sokolíku.
Píšeš
z matematickýho hlediska je tedy VESMÍR (jakožto kontinuum) STEJNĚ VELIKEJ JAKO TŘEBA JABKO. Což ovšem evidentně není pravda. Už jen ten výraz,
"věc je stejně mohutná jako její část", naznačuje jakousi odtrženost od reality.
Matematické hledisko "velikosti" postavené na porovnávání "počtu prvků" (mohutnosti) množin není jediným možným hlediskem, s nimiž matematika pracuje.
Jiným hlediskem by mohlo být hledisko metrické (tenká tyč délky 1m by byla větší než koule o průměru pouze 99 cm),
dalším hlediskem by mohlo být hledisko objemu , případně hmotnosti a pod.
Chceme-li být při zkoumání vesmíru "v souladu s realitou", musíme ke každé zkoumané situaci volit adekvátní hledisko.
Mimochodem: smyslem onoho hlediska mohutnosti je porovnávat nekonečné množiny. Například množinu všech přirozených čísel je možno zobrazit
vzájemně jednoznačně na množinu všech celých čísel a dokonce i na množinu všech racionálních čísel, ale ne už na množinu všech reálných čísel.
Znamená to, že "nekonečno" vyjadřující množství reálných čísel není stejné jako "nekonečno" vyjadřující množství přirozených čísel.
Offline
#8 16. 04. 2012 18:16
- Sokolik
- Příspěvky: 27
Re: Struktura izomorfní s vesmírem
↑ Rumburak:
Doufal jsem, že bude z kontextu poznat, že nepotřebuju vysvětlovat triviální fakta o mohutnosti množin. Jinak máš určitě pravdu, že různý hlediska reality se popisujou různýma matematickýma nástroji, tedy např. rozlehlost se popisuje metrikou.
Ovšem nekonečný kontinuum s metrikou je sice jiná struktura než konečný kontinuum s metrikou (konečný ve smyslu vzdálenosti), ale na stejný množině individuí! Čili relace kolem vzdálenosti jsou tam jinak uspořádaný, a to je vše, čím se tyhle dvě struktury liší. Vesmír pak není složitější než jablko, jenom je jinak uspořádanej! Metrika mu nedává žádnou složitost navíc. Nebo ano?
Offline
#9 17. 04. 2012 09:46 — Editoval Rumburak (17. 04. 2012 15:40)
Re: Struktura izomorfní s vesmírem
↑ Sokolik:
I když proti filosofům nic nemám, domnívám se, že se dopouštějí chyby, pokud se snaží s vágními pojmy jako je "složitost vesmíru"
nebo "uspořádání vesmíru" a podobně zacházet exaktně.
Definuj, jak měřit složitost vesmíru a složitost jablka - teprve pak možno okolo toho něco řešit.
Offline
#10 17. 04. 2012 15:09
Re: Struktura izomorfní s vesmírem
↑ Sokolik:
Téměř na fórum nepřispívám, ale jsem tu každý den, takže mi asi nepřísluší navrhnout tě na cenu Bludný balvan
Offline
#12 18. 04. 2012 03:11
- Sokolik
- Příspěvky: 27
Re: Struktura izomorfní s vesmírem
↑ Rumburak:
V tom nejzákladnějším smyslu není složitost věci nic jinýho než množství jejích částí.
Je to pojem logicky dosti přesný - věř mi, že většina pojmů ze života je mnohem vágnějších.
A víš co, já už jsem smířen se zjištěním, že všechny věci jsou ve svý podstatě nejspíš stejně složitý, nezávisle na jejich velikosti. A taky s tím, že na tomhle fóru není zvykem diskutovat o problémech, u kterých se zdá, že nemají jedno jasné "řešení". Takže tobě díky za pokec, téma zavírám.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Struktura izomorfní s vesmírem (TOTO TÉMA JE VYŘEŠENÉ)
