Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 04. 2012 17:49
koule - statistika
Pěkný den,
prosil bych jestli by mi někdo pomohl s tímto příkladem, nějak nevím kde mám začít. Aspon jak si nadefinuji ty pravděpodobnosti pro vytažení modré koule?
Děkuji moc za pomoc
V krabici je pět bílých a tři modré koule.
1. Určete pravděpodobnostní a distribuční funkci náhodné veličiny X, popisující počet
pokusů nutných k vytažení modré koule.
Děkuji moc za pomoc
Offline
#2 19. 04. 2012 19:46
Re: koule - statistika
ahoj ↑ jendula11:
vytiahnutú guľu vraciaš po každom pokuse naspäť do krabice?
alebo ostane vonku?
Offline
#4 20. 04. 2012 16:57
Re: koule - statistika
s↑ jendula11:
povedzme že máme v krabici 1 bielu a 2 modré
chceme nájsť pravdepodobnostnú funkciu a distribučnú funkciu veličiny X popisujúcu počet pokusov potrebných
na vytiahnutie modrej s tým že vytiahnuté ostanú vonku
spôsoby ako gule vytiahnuť z krabice sú tieto: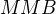
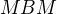
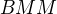 (MBM znamená prvá vytiahnutá je modrá, druhá biela, tretia modrá)
(MBM znamená prvá vytiahnutá je modrá, druhá biela, tretia modrá)
teda 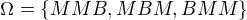 pričom
pričom 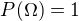
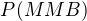 je pravdepodobnosť, že ako prvá bude vytiahnutá modrá (z 2 modrých a jednej bielej), ako druhá modrá (z 1 bielej a 1 modrej) a ako tretia biela (z jednej bielej) teda
je pravdepodobnosť, že ako prvá bude vytiahnutá modrá (z 2 modrých a jednej bielej), ako druhá modrá (z 1 bielej a 1 modrej) a ako tretia biela (z jednej bielej) teda
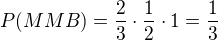
podobne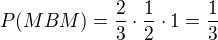
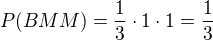
vidno že počet pokusov na vytiahnutie modrej je najmenej 1 a najviac 2,
to sú hodnoty ktoré nadobúda  definovaná na množine
definovaná na množine  , pričom
, pričom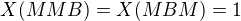 a
a 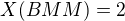
takže pravdepodobnostná funkcia bude:![kopírovat do textarea $P:\{1,2\}\rightarrow [0,1]$](/mathtex/64/646e0f1f8b09bc6375d57e7d868da975.gif)
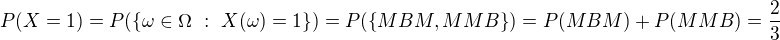
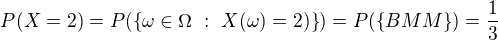
pravdepodobnostnú funkciu máme,
môžme urobiť distribučnú funkciu ![kopírovat do textarea $F:\mathbb{R}\rightarrow [0,1]$](/mathtex/a6/a654e6b9b21e3229195c2f51648bd919.gif)
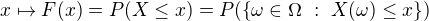
keďže 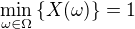 tak bude
tak bude 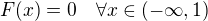
a z 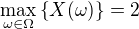 máme
máme 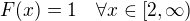
na intervale 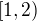 bude
bude 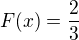
takto isto sa to dá spočítať aj v tvojom príklade, len je tam trochu viac počítania, lebo tam môže byť pokusov od 1 do 6 a množina  je väčšia
je väčšia
Offline
