Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Konvergence integrálu (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 04. 2012 20:11
Konvergence integrálu
Ahoj,
řeším příklad na konvergenci určitého zobecněného Riemannova integrálu 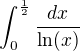 , ale protože je integrand záporný, tak nemůžu použít srovnávací kritérium. Stroj umí integrál numericky vyřešit, ale ani samotnému se mi nepodařilo žádnou metodou určit primitivní funkci.
, ale protože je integrand záporný, tak nemůžu použít srovnávací kritérium. Stroj umí integrál numericky vyřešit, ale ani samotnému se mi nepodařilo žádnou metodou určit primitivní funkci.
Jak bych mohl jinak dokázat, že integrál konverguje?
Offline
- (téma jako vyřešené označil(a) Sulfan)
#2 22. 04. 2012 00:09
Re: Konvergence integrálu
ahoj ↑ Sulfan:
mám pocit že primitívna funkcia sa v tomto prípade nedá vyjadriť pomocou elementárnych funkcií
mohlo by fungovať niečo takéto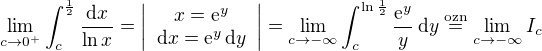
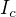 je síce záporné číslo pre každé
je síce záporné číslo pre každé  , ale konečné
, ale konečné
integrand je všade záporný, takže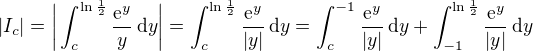
v medziach  a
a 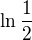 ide o spojitú funkciu na kompakte, jej integrál sa dá určite zhora ohraničiť konštantou
ide o spojitú funkciu na kompakte, jej integrál sa dá určite zhora ohraničiť konštantou  ,
,
limita na tento integrál nemá vplyv
na intervale ![kopírovat do textarea $[c,-1]$](/mathtex/02/024f04755df4f321d96dc4cb5e3ffbef.gif) je
je 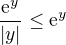 pričom rovnosť nastane len v
pričom rovnosť nastane len v 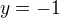 ,
,
teda  a integrál konverguje
a integrál konverguje
Offline
#3 22. 04. 2012 00:36 — Editoval Pavel Brožek (22. 04. 2012 00:38)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konvergence integrálu
↑ Sulfan:
Když ti dělá problém, že je integrand záporný, věděl by sis rady s 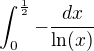 ?
?
↑ jardofpr:
Nestačilo by původní funkci 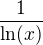 dodefinovat v nule nulou a měli bychom spojitou funkci na kompaktu rovnou?
dodefinovat v nule nulou a měli bychom spojitou funkci na kompaktu rovnou?
Offline
#4 22. 04. 2012 09:30 — Editoval Sulfan (22. 04. 2012 09:31)
Re: Konvergence integrálu
↑ jardofpr: Děkuji za vysvětlení, mohu se ale zeptat, jakou větu využíváme, když řekneme, že funkce je spojitá "na kompaktu" (uzavřený interval?), tak je i její integrál na tomto intervalu omezený?
↑ Pavel Brožek: To bych zkusil takto, nešlo by například říci: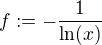
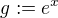
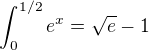
a protože 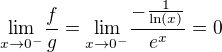

Offline
#5 22. 04. 2012 09:44
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konvergence integrálu
↑ Sulfan:
Proč zrovna 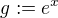 a ne
a ne 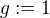 ?
?
Offline
#6 22. 04. 2012 10:49
Re: Konvergence integrálu
ahoj ↑ Pavel Brožek:
stačilo, a z môjho komplikovaného výpočtu sa stane jednoriadkové zdôvodnenie ..
ešte aj to ohraničenie bude potom zrejme lepšie, vďaka za postreh :)
↑ Sulfan:
v metrickom priestore je kompaktná množina taká množina K, že ľubovoľná postupnosť prvkov z K obsahuje podpostupnosť, ktorej limita leží v K
uzavretý interval v  je kompakt
je kompakt
(v euklidovskom priestore by to mali byť uzavreté a ohraničené množiny)
spojitá funkcia na kompaktnej množine nadobúda na tejto množine maximum aj minimum
v mojom postupe to bol interval ![kopírovat do textarea $[-1,\ln{1/2}]:=I$](/mathtex/ae/ae4ef547a05beb958e474aae24335041.gif)
tam 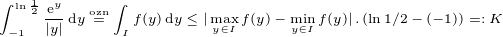
Offline
#7 22. 04. 2012 11:11
Re: Konvergence integrálu
↑ Pavel Brožek: Jo aha, no to asi kvůli mému profilovému obrázku :). Každopádně - je to korektní ?
↑ jardofpr: Děkuji, teď je mi to již jasné.
Offline
#8 22. 04. 2012 11:42
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konvergence integrálu
↑ Sulfan:
Nevzpomínám si na přesné znění věty, kterou používáš, takže nemůžu říct, že to je korektní.
Offline
#9 22. 04. 2012 12:54
Re: Konvergence integrálu
↑ Pavel Brožek: Vycházel jsem z:
Buďte  ,
, 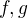 nezáporné funkce na
nezáporné funkce na  tak, že existují vlastní
tak, že existují vlastní 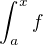 a
a 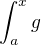
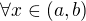 a zároveň
a zároveň 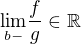 . Pak platí:
. Pak platí: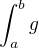 konverguje
konverguje  konverguje.
konverguje.
Offline
#10 22. 04. 2012 13:21
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konvergence integrálu
↑ Sulfan:
Pak je to podle mě korektní.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Konvergence integrálu (TOTO TÉMA JE VYŘEŠENÉ)