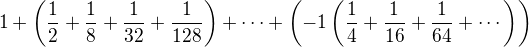Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 23. 04. 2012 20:50 — Editoval Honza Matika (23. 04. 2012 20:51)
#3 23. 04. 2012 20:58 — Editoval martanko (23. 04. 2012 21:01)
Re: nekonecny rad
↑ Honza Matika:
na tie dve rady som si to aj rozdelil no takto mi to vychadza 4/3 a nie 6/5 tak som si neni isty ci je to dobre
edit: pripadne vies ako to napisat do wolfram math? neviem tam napisat nekonecny rad ze by som si overil postup
Offline
#4 23. 04. 2012 21:10
Re: nekonecny rad
Do Wolframu napiš:
1+sum(-1/((-2)^(k)),k,1,inf)
inf znamená nekonečno (místo něj můžeš napsat konkrétní číslo, případně proměnou)
Offline
#5 23. 04. 2012 21:10
- skoroakvarista

- Místo: Praha
- Příspěvky: 299
- Škola: FJFI ČVUT - ASI
- Pozice: Student
- Reputace: 20
Re: nekonecny rad
↑ martanko:
Zdravím, ono to má opravdu vyjít 4/3. Do wolframu napiš "1 + (1/2)sum (-1)^k/2^k for k from 0 to infinity"
Offline
 viem ze to ma byt
viem ze to ma byt  no neviem sa dopracovat k postupu, ratam to uz asi tri hodiny.. dik za pomoc
no neviem sa dopracovat k postupu, ratam to uz asi tri hodiny.. dik za pomoc