Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 04. 2012 21:52
analytická geometrie
Dobrý den,
mám parametr. zadanou přímku  v prostoru:
v prostoru: 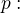



Při jakém  platí
platí  , kde
, kde  je rovina a platí pro ní:
je rovina a platí pro ní:  .
.
Směrový vektor přímky  je tedy
je tedy  a normálový vektor roviny
a normálový vektor roviny  je
je  . A teď nevím jak dál, protože v prostoru je nekonečně mnoho kolmých vektorů. Nebo zvolit jiný postup, moje úvaha tvrdí, že jsou-li směrové vektory lineárně závislé, jsou přímka s rovinou rovnoběžné.
. A teď nevím jak dál, protože v prostoru je nekonečně mnoho kolmých vektorů. Nebo zvolit jiný postup, moje úvaha tvrdí, že jsou-li směrové vektory lineárně závislé, jsou přímka s rovinou rovnoběžné.
Offline
- (téma jako vyřešené označil(a) APavlat)
#2 23. 04. 2012 22:15
Re: analytická geometrie
↑ APavlat:
hned zítra ráno vyzkouším vektorový součin  a
a  položit nule. To by mohlo být řešení.
položit nule. To by mohlo být řešení.
Offline
#3 23. 04. 2012 22:37
Re: analytická geometrie
↑ APavlat:
Dobrý večer,
takto zadaná přímka je rovnoběžná s rovinou, je-li její směrový vektor 
kolmý na normálový vektor roviny  .
.
A dva vektory jsou navzájem kolmé, je-li jejich skalární součin roven nule ... :)
Offline
