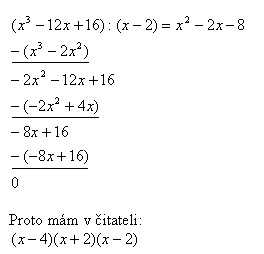Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 05. 2012 08:31
- American_pie
- Příspěvky: 45
- Reputace: 0
Re: Limita
žiadneho L Hospitala netreba :-) ...
citatel rozložiť na tvar: (x-2)^20 * (x+1)^20
jmenovatel podelit najprv (x-2), potom rozložiť polynom x^2 + 2x - 8 ...
čili v menovateli dostanes pňnapokon: (x-2)^10 * (x+4)^10 * (x-2)^10
pokrátiš s čitatelom a dostávaš limitu z (x+1)^20 / (x+4)^10 .... po dosadení dvojky je to 3^20 / 6^10 = 3^10 / 2^10 =:VYSLEDOK LIMITY.
všetko jasné? :-)
Offline
#3 05. 05. 2012 08:32 Příspěvek uživatele Sulfan byl skryt uživatelem Sulfan.
#5 06. 05. 2012 09:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ leniczcha:
zdravím,
jmenovatel také rozložit na součin - pomůže upravit po dvojicích 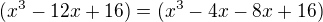 (nebo jak doporučuje kolega - zkusit uhodnout jeden kořen (x=2) a podělit mnohočlen dvoučlenem pro další rozklad. Pořádku? Děkuji.
(nebo jak doporučuje kolega - zkusit uhodnout jeden kořen (x=2) a podělit mnohočlen dvoučlenem pro další rozklad. Pořádku? Děkuji.
Offline
#7 06. 05. 2012 14:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ leniczcha:
pokračuj, prosím, vytykat:
Offline
#9 06. 05. 2012 14:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ leniczcha:
není za co. Ano, vydělit můžeš, jen pozor na mocniny, co jsou u jednotlivých závorek v čitateli a v jmenovateli.
Offline
#11 06. 05. 2012 17:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ leniczcha:
asi nějaka nepozornost při rozkladu - kontrola.
tedy v jmenovateli je výsledek, jak již uváděl kolega ↑ American_pie: 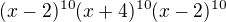 to už se podaří.
to už se podaří.
Offline
#15 07. 05. 2012 09:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ leniczcha:
protože jsi nezměnila znaménko -(... -2x^2) na 2. řádku dává 2x^2 na 3. radku. Už v pořádku? Děkuji.
Offline
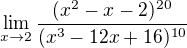
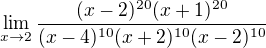

 souhlasí?
souhlasí?