Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » cramerovo pravidlo (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 12. 2007 10:25
cramerovo pravidlo
Dobrý den, moc nekoho prosim, aby mi mohl vypocitat tyto priklady.
Pomocí cramerova pravidla nalezněte řešení systémů rovnic zadaných rozšířenou maticí
3 1 -1 / 1
2 -1 1 /1
2 1 0 /1
a
1 2 1 -1 / 1
1 4 2 1 / 2
1 2 3 0 / 2
0 1 3 3 / 1
mockrat děkuji
Offline
#2 05. 12. 2007 21:14 — Editoval Marian (05. 12. 2007 21:16)
Re: cramerovo pravidlo
Jestlize umis pocitat determinanty, pak to prece nemuze byt problem. Pouziti Cramerova pravidla byva zpravidla dobre popisovano ve skriptech.
Nejprve zjistis (overis), jestli jsou tyto soustavy resitelne cramerovsky. To udelas tak, ze spocitas determinant matice soustavy (ten prvni bude tretiho radu, u druheho prikladu ctvrteho radu).. Pokud vyjde ruzny od nuly, oustava je cramerovsky resitelna. V opacnem pripade nelze pouzit Cramerovo pravidlo.
Vemu pro jednoduchost prvni z tech soustav (predpokladam, ze je cramerovsky resitelna). Chces li spocist prvni neznamou (asociovanou s prvnim sloupcem rozsirene matice soustavy), "prepis" prvni sloupec matice soustavy (je typu 3x3) tim zpusobem, ze jej nahradis sloupcem pravych stran. Druhy a treti sloupec zustava nezmeneny. Vznika jakasi matice, oznacim ji treba A_1, jeji determinant oznacim det(A_1). Pak neznama, rekneme x_1 (asociovana s prvnim sloupcem matice soustavy) je dana vzorcem
x_1=det(A_1)/det(A).
Stejne spoctes i ostatni nezname, jen misto prvniho slopce budes v pripade vypoctu nezname x_2 nahrazovat pravymi stranami sloupec druhy. Pro x_3 analogicky.
Pro vypocet i-te nezname zkonstruujes matici A_i a pouzijes vztahu
x_i=det(A_i)/det(A).
Offline
#3 05. 12. 2007 21:35 — Editoval Saturday (21. 05. 2012 18:52)
Re: cramerovo pravidlo
Ten druhý příklad není těžký, samotné Cramerovo pravidlo je jednoduché, jediný problém je v determinantu 4. stupně.
Vezmu to popořádě:
1) označme si zadanou matici (A|b), kde A je matice daná koeficienty neznámých u lineárních rovnic soustavy a "b" je vektor pravých stran soustavy rovnic:
2) Cramerovo pravidlo nám říká, jak vypadá řešení soustavy n lineárních rovnic o n neznámých. Nejdříve je třeba vypočítat determinant  , pokud je determinant nulový, pak soustava rovnic nemá jednoznačné řešení. Pak je třeba vypočítat determinanty matic, které vzniknou tak, že zaměním i-tý sloupec za sloupec pravých stran. Takto vzniklá matice se označuje
, pokud je determinant nulový, pak soustava rovnic nemá jednoznačné řešení. Pak je třeba vypočítat determinanty matic, které vzniknou tak, že zaměním i-tý sloupec za sloupec pravých stran. Takto vzniklá matice se označuje  (dohromady je tedy třeba spočítat n+1 determinantů)
(dohromady je tedy třeba spočítat n+1 determinantů)
Ještě před počítáním determinantů je třeba si říct, jak se spočítá hodnota determinantu - jde to několika způsoby, já to ukážu to pomocí Gaussovy eliminace (tzn. snaha o převod matice na trojúhelníkový tvar se zachováním hodnoty determinantu)
Vlastnosti při počítání determinantu:
1) determinant jednotkové matice je 1
2) výměnou libovolných dvou řádků matice se změní znaménko determinantu
3) má-li matice libovolné dva řádky stejné, pak její determinant je nulový
4) vynásobením libovol. řádku matice nenulovým skalárem (číslem)  se determinant příslušné matice zvětší
se determinant příslušné matice zvětší  -krát
-krát
5) determinant singulární matice je nulový, determinant regulární matice je nenulový
Takže vzhůru k počítání prvního determinantu:
vysvětlení úprav determinantu na trojúhelníkový tvar:
- v druhém kroku jsme zaměnili čtvrtý a druhý řádek, proto jsme museli determinant vynásobit -1, protože podle pravidel výše dochází ke změně znaménka determinantu
- ve třetím kroku jsme vynásobili třetí a čtvrtý řádek -1 a přičetli k oboum první řádek - čímž jsme nezměnili hodnotu determinantu
- ve čtvrtém kroku jsme přičetli dvojnásobek druhého řádku ke čtvrtému a pak jsme vynásobili třetí řádek pětko a čtvrtý řádek dvojkou a pak jsme třetí a čtvrtý řádek sečetli -> nyní jsme však provedli úpravu, která změnila hodnotu determinantu - a proto podle pravidla 4) musíme vydělit celý výraz pětkou a dvojkou (což je to samé jako násobení převrácenou hodnotou čísel)
a nyní se vynásobí prvky na diagonále (proto se celá Gaussova eliminace dělá; pokud máme matici ve trojúhelníkovém tvaru a vynásobíme členy na diagonále, dostaneme determinant matice) -> dostáváme -30; determinant je tedy: (-1) * 1/5 * 1/2 *(-30) = 3 = det A (EDIT: CHYBA: místo -30 má být -80. - Děkuji za upozornění)
nyní je třeba vypočítat: 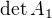 ,
, ,
, ,
,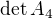
...
výpočet je to sice pracný, ale je podle mě lepší než výpočet pomocí rozvoje daného sloupce nebo řádku proto, že ten už není moc vhodný pro determinanty stupně většího než 4.
Zpět ke Cramerovu pravidlu, Cramerovo pravidlo říká, že 
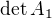 vyjde -9
vyjde -9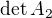 vyjde 3
vyjde 3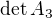 vyjde 3
vyjde 3 vyjde -3
vyjde -3
řešením soustavy je tedy vektor: [-3,1,1,-1]
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#4 06. 01. 2008 13:47
Re: cramerovo pravidlo
Prosim, mam mensi dotaz ke Cramerovu pravidlu...
Je soustava "Cramerovsky resitelna" pokud hlavni determinant vyjde "nenulovy", determinant A1 taky, ale determinanty A2,A3 vyjdnou "nulove" a determinant A4 vyjde "-2" ...
Nejak se mi tam nelibi ty nuly... Priklad jeste nemam dopocten uplne (hodnoty jednotlivych promenych), jelikoz nevim zda ma smysl pocitat dale...
Dekuji, santic
Offline
#5 06. 01. 2008 13:51
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: cramerovo pravidlo
santic napsal(a):
Prosim, mam mensi dotaz ke Cramerovu pravidlu...
Je soustava "Cramerovsky resitelna" pokud hlavni determinant vyjde "nenulovy", determinant A1 taky, ale determinanty A2,A3 vyjdnou "nulove" a determinant A4 vyjde "-2" ...
Nejak se mi tam nelibi ty nuly... Priklad jeste nemam dopocten uplne (hodnoty jednotlivych promenych), jelikoz nevim zda ma smysl pocitat dale...
Dekuji, santic
pokud je nektera neznama rovna nule - a to se muze stat - tak prislusny deteminant je taky nula. Takze nevadi, pocitejte dal. Hlavne nesmi byt nula ten determinant matice soustavy - jinak by se muselo pouzit zobecnene Cramerovo pravidlo.
Offline
#6 06. 01. 2008 13:53
Re: cramerovo pravidlo
robert.marik napsal(a):
santic napsal(a):
Prosim, mam mensi dotaz ke Cramerovu pravidlu...
Je soustava "Cramerovsky resitelna" pokud hlavni determinant vyjde "nenulovy", determinant A1 taky, ale determinanty A2,A3 vyjdnou "nulove" a determinant A4 vyjde "-2" ...
Nejak se mi tam nelibi ty nuly... Priklad jeste nemam dopocten uplne (hodnoty jednotlivych promenych), jelikoz nevim zda ma smysl pocitat dale...
Dekuji, santicpokud je nektera neznama rovna nule - a to se muze stat - tak prislusny deteminant je taky nula. Takze nevadi, pocitejte dal. Hlavne nesmi byt nula ten determinant matice soustavy - jinak by se muselo pouzit zobecnene Cramerovo pravidlo.
Ok, diky moc... Jen jsem nevedel jestli ma smysl pocitat dale, jelikoz toho musim dnes stihnout jeste celkem haffo, tak neni zavhodno se cimkoli zdrzovat ;)
Offline
#7 09. 12. 2011 13:37
Re: cramerovo pravidlo
↑ Saturday:
Pěkně vysvětleno, akorát jak se tak divám:
pokud máme matici ve trojúhelníkovém tvaru a vynásobíme členy na diagonále, dostaneme determinant matice) -> dostáváme -30
Nemá být náhodou součin členů na diagonále 1*1*(-10)*8 = -80 ?
Offline
#9 21. 05. 2012 18:53
Re: cramerovo pravidlo
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » cramerovo pravidlo (TOTO TÉMA JE VYŘEŠENÉ)
