Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Určete limity funkcí (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 06. 2012 23:32
Určete limity funkcí
Dobrý den je o dva příklady na limity funkcí.
1) Jedná se o takový to tvar:![kopírovat do textarea $\lim_{x\to2}[8/(x^{2}-4)-2/(x-2)]$](/mathtex/75/75582155c25e10d3d8f45e66b19851e6.gif)
Výsledek by měl vyjít -1/2. Bohužel k tomuto výsledku jsem se za pomocí sloučení zlomků a dosazeni nedopracoval.
2) Tento příklad jde vypočítat l´Hospitalem velice jednoduše, chtěl jsem se jen zeptat jaké úpravy by člověk měl použít aby se dopracoval výsledku bez l´Hospitala.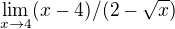
výsledek: -4
Děkuji za pomoc. Jde mi jen o naučení se či poupravení postupů při řešení úloh.
Offline
- (téma jako vyřešené označil(a) jelena)
#3 01. 06. 2012 23:51
Re: Určete limity funkcí
V obou prikladech je potreba vhodne pouzit vzorec 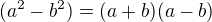
Ad 1)
Po prevedeni na spolecny jmenovatel by jsi mel mit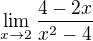 a prave pomoci toho vzorce to vykratit...
a prave pomoci toho vzorce to vykratit...
Ad2)
Tady je to uplne analogicke, jen se rozklada citatel a ne jmenovatel.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Určete limity funkcí (TOTO TÉMA JE VYŘEŠENÉ)