Matematické Fórum

vviston · 07. 06. 2012 10:56

Mějme v rovině 6 bodů, z nichž žádné tři neleží na jedné přímce. Spojíme náhodně vybrané 3 dvojice úsečkou. Jaká je pravděpodobnost, že vznikne trojúhelník, jestliže a) dvojice se ve výběru mohou opakovat
b) dvojice se ve výběru nemohou opakovat

Já jsem se dostal k tomu že všechny možné kombinace jsou 6 nad 2 to jsou všechny možné dvojice, ale za boha nemůžu přijít na to, jak dostanu číslo které se rovná příznivým možnostem...takže mám jen zlomek něco lomeno (6 nad 2) na třetí. Poradíte ?:P

OiBobik

↑ vviston:

Ahoj,

zkus se na to dívat takto:

Každý výběr trojice úseček takový, že vznikne trojúhelník, lze popsat tak, že se prvně zvolí tři vrcholy (= vrcholy budoucího trojúhelníka) a na nich se pak některým z možných pořadí vyberou postupně všechny tři potřebné úsečky.

Pak by neměl být problém spočítat počet příznivých jevů pro (a) a zároveň i pro (b). Pro (b) je třeba ještě zvlášť spočítat počet všech možných jevů.

Honzc · 07. 06. 2012 14:04 — Editoval Honzc (07. 06. 2012 14:04)

↑ vviston:
Zkus si nakreslit pravidelný šestiúhelník a pak
a) udělat všechny úhlopříčky a spočítat si jednak kolik je spojnic dvou bodů (to už máš) a kolik z nich tvoří trojúhelník
b)zkus sám

vviston · 07. 06. 2012 15:06

Ty jo tak pořád nějak nevím...v řešení je v čitateli 15 * 8 * 1 a vespodu je 15^3 pořád přemýšlím jak přisli na 15 pak 8 a pak 1 :D opravdu to nevidím, pokud to jde, kopněte mě silněji!! Díky :/

OiBobik

↑ vviston:

Vychází jim to přesně v souladu s mým návodem, jen nevím, proč tak podivně sdružovali čísla.

Trochu formálněji:

(a) Očíslujme body v rovině čísly 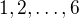$1,2, \dots,6$ . Pravděpodobnostní prostor, který budeme uvažovat, je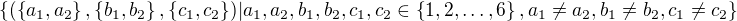 $\{(\{a_1,a_2\},\{b_1,b_2\},\{c_1,c_2\})| a_1,a_2,b_1,b_2,c_1,c_2 \in \{1,2, \dots,6\}, a_1 \neq a_2, b_1 \neq b_2, c_1 \neq c_2 \}$

Neboli: děláme uspořádaný výběr tří neuspořádaných dvojic bodů.

Velikost celého toho prostoru je 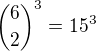${6 \choose 2}^3=15^3$ , jaks už spočítal.

Teď je třeba spočítat příznivé jevy: To znamená, určit velikost množiny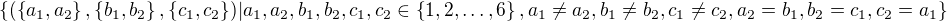
$\{(\{a_1,a_2\},\{b_1,b_2\},\{c_1,c_2\})| a_1,a_2,b_1,b_2,c_1,c_2 \in \{1,2, \dots,6\}, a_1 \neq a_2, b_1 \neq b_2, c_1 \neq c_2, a_2=b_1, b_2=c_1, c_2=a_1 \}$

No a návod jak na to, jsem již podal výše: Zkus prvně spočítat, kolika způsoby lze vybrat trojici vrcholů trojúhelníka (podmínky 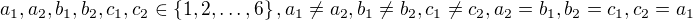$a_1,a_2,b_1,b_2,c_1,c_2 \in \{1,2, \dots,6\}, a_1 \neq a_2, b_1 \neq b_2, c_1 \neq c_2, a_2=b_1, b_2=c_1, c_2=a_1$ implikují 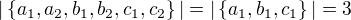$|\{a_1,a_2,b_1,b_2,c_1,c_2\}|=|\{a_1,b_1,c_1\}|=3$ ) a potom počet možných pořadí, jakými mohly být hrany trojúhelníka vybrány.

Matematické Fórum

#1 07. 06. 2012 10:56

Kombinatorika - jsem mimo :D

#2 07. 06. 2012 13:15 — Editoval OiBobik (07. 06. 2012 13:17)

Re: Kombinatorika - jsem mimo :D

#3 07. 06. 2012 14:04 — Editoval Honzc (07. 06. 2012 14:04)

Re: Kombinatorika - jsem mimo :D

#4 07. 06. 2012 15:06

Re: Kombinatorika - jsem mimo :D

#5 07. 06. 2012 17:50 — Editoval OiBobik (07. 06. 2012 18:04)

Re: Kombinatorika - jsem mimo :D

Zápatí