Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » algebraická uzavretosť algebraických čísel
#2 09. 06. 2012 11:41 — Editoval OiBobik (09. 06. 2012 15:19)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: algebraická uzavretosť algebraických čísel
↑ jarrro:
Ahoj, musí:
Nechť 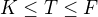 jsou tělesa,
jsou tělesa, 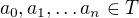 prvky algebraické nad
prvky algebraické nad  a
a 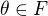 je kořen polynomu
je kořen polynomu ![kopírovat do textarea $f=\sum_{k=0}^n a_k x^k \in T[x]$](/mathtex/0c/0c1174b576263a2f07de4bc50e1b2ce0.gif) . Pak
. Pak ![kopírovat do textarea $[K(a_0,a_1 \dots a_n,\theta):K]=[K(a_0,a_1 \dots a_n,\theta):K(a_0,a_1 \dots a_n)]\cdot[K(a_0,a_1 \dots a_n):K]$](/mathtex/b1/b1e73917b8042c2a69331b73b61f8950.gif) .
.
Přitom ![kopírovat do textarea $[K(a_0,a_1 \dots a_n,\theta):K(a_0,a_1 \dots a_n)] < \infty$](/mathtex/15/15e439067e38f07b49c38d603c32a769.gif) (jelikož
(jelikož  je algebraický nad
je algebraický nad 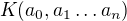 )
)
a ![kopírovat do textarea $[K(a_0,a_1 \dots a_n):K]<\infty$](/mathtex/6d/6de706214a734b4347d6e631a50cad80.gif) (prvky
(prvky 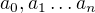 jsou algebraické nad
jsou algebraické nad  ).
).
Celkem tedy 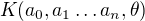 je rozšíření
je rozšíření  konečného stupně, tedy algebraické rozšíření.
konečného stupně, tedy algebraické rozšíření.
Značení (nevím, nakolik je to, co používám, běžné, tak radši píšu):
Využívá se:
EDIT: všechna tělesa předpokládám komutativní
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#4 09. 06. 2012 13:02 — Editoval OiBobik (09. 06. 2012 13:53)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: algebraická uzavretosť algebraických čísel
↑ jarrro:
No, tak to nevím. To bude takto obecně asi dost obtížné, bude-li to vůbec možné (tím myslím: nějak přímo z polynomů, které nulují jednotlivé koeficienty, vykřesat polynom, který nuluje kořen onoho polynomu s algebraickými koeficienty).
Nicméně (nevím, jestli jsi někdy tady ty pojmy už viděl, ale i kdyby ne, tak) ta použitá tvrzení nejsou moc hluboká a všechny ty důkazy najdeš třeba zde, zejména asi v kapitole 9.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » algebraická uzavretosť algebraických čísel
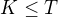 tělesa, pak
tělesa, pak ![kopírovat do textarea $[T:K]$](/mathtex/29/29cea9602aa77298ede0fb03551a03cd.gif) značí stupeň rozšíření
značí stupeň rozšíření  (
(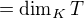 , když chápu
, když chápu 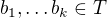 , pak
, pak 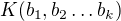 je nejmenší nadtěleso
je nejmenší nadtěleso 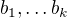 .
.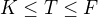 tělesa, pak
tělesa, pak ![kopírovat do textarea $[F:K]=[F:T]\cdot[T:K]$](/mathtex/8b/8b4cbf5ff5d2372556a281e08a74d511.gif) .
.