Matematické Fórum

vanok · 13. 06. 2012 14:48 — Editoval vanok (13. 06. 2012 15:00)

↑↑ Rumburak:,
Pozdravujem, ano toto je trosicku ina cesta k rieseniu.
Pozriem to podrobne vecer.

Inac tu je tiez jedna odpoved v okoli nuly pre funkciu, co znacim F:
http://www.wolframalpha.com/input/?i=1% … 28X%2B4%29

EDIT

↑↑ vanok:
pisal som :
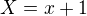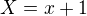Tak najprv poloz $X=x+1$ cize $x=X-1$ , a nahrad to v tvojej funkcii, co ti povoli pouzit rozvoj okolo nuly $F(X)$ ,( premenna je potom X) a po vypoctoch nahrad vsade $X=x+1$ ( co da hladany rozvoj )
Tak zacnime: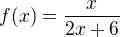
$f(x) = \frac{x}{2x+6}$
ti da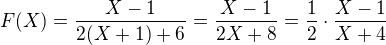
$F(X)=\frac{X-1}{2(X+1)+6}= \frac {X-1}{2X+8}=\frac 12 \cdot \frac {X-1}{X+4}$

No vsak vidim ze som mal napisat: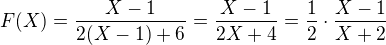

$F(X)=\frac{X-1}{2(X-1)+6}= \frac {X-1}{2X+4}=\frac 12 \cdot \frac {X-1}{X+2}$
(spatne znamienko v povodnom vyraze )

Cize vypocty,co som navrhol boli robene na chybnom vyraze.

OiBobik

↑↑ darkmagic:

Zdravím,
navrhl bych ještě alternativní postup, a sice pomocí rozvoje funkce do Taylorovy řady.

Pomocí úpravy $\frac{x}{2x+6}=\frac{1}{2}-\frac{3}{2}\cdot (x+3)^{-1}$

se snadno (indukcí) odvodí, že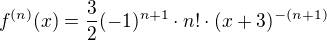
$f^{(n)}(x)=\frac{3}{2}(-1)^{n+1} \cdot n!\cdot(x+3)^{-(n+1)}$
tedy
$f^{(n)}(-1)=\frac{3}{2}(-1)^{n+1} \cdot n!\cdot(2)^{-(n+1)}=\frac{3}{2}(-1)^{n+1} \cdot n!\cdot\frac{1}{2^{n+1}}$

odtud dostáváme jediného kandidáta na rozvoj do řady

$-\frac{1}{4}+\sum_{n=1}^{\infty}\frac{f^{(n)}(-1)}{n!}(x+1)^n=-\frac{1}{4}+\frac{3}{2}\sum_{n=1}^{\infty}$\frac{-1}{2}$^{n+1}(x+1)^n$

- jediný kandidát je to z toho důvodu, že mocninné řady lze derivovat člen po členu.

tento přístup má ovšem jednu nevýhodu, a sice: není zaručeno, že opravdu zadaná funkce do mocninné řady rozvinout lze (existují i nekonečně diferencovatelné funkce, které nelze rozvinout do mocninné řady). Muselo by se tedy např. výslednou řadu opět sečíst a ukázat, že dostanu původní funkci, což mi ovšem připadá jako jednodušší úloha.

EDIT: Vidím, že během mého spisování už i Rumburak přidal nějaké alternativní řešení - pokud se vám zdá, že je tu toho už moc, tak se smažu. Alespoň jsem však ověřil Rumburakův výsledek.

Rumburak · 13. 06. 2012 15:27

↑ OiBobik:
Ahoj,
děkuji Ti za ověření "mého" výsledku další metodou. :-)
Když je ukázáno více metod, já osobně proti tomu vůbec nic nemám, naopak to považuji za užitečné a mnohdy i velmi zajímavé až fascinující -
snad právě díky takovým možnostem mě matematika baví.

darkmagic

Snažil jsem se to udělat podle rad, co jsem zde dostal. Teď přijímám podněty k případným chybám :).
Vycházel jsem především z toho, co jsme řešili s ↑↑ vanok:.

Pro přehlednost:

Autor skryl část textu. Zobrazit/skrýt!