Matematické Fórum

zdenekm31 · 15. 06. 2012 13:16

Dobrý den,
mam problém s triviálnim příkladem na výpočet těžiště, mam pomocí integrálu vypočíat těžiště jednotkového půlkruhu...

Základní vzorce mam z více zdrojů, ale na žádném se mi neshodují, tak abych je mohl použít a byl si jist že je to správně,

$x^{2}+y^{2}=r^{2}$ tudíž by to mělo být: $y= \sqrt{x^{2}-r^{2}}$

Vzorce co nám nadiktovali učitelé jsou: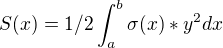
$S(x) = 1/2\int_{a}^{b}\sigma (x)*y^{2}dx$
$S(y) = \int_{a}^{b}\sigma (x)*y*x dx$
$m = \int_{a}^{b}\sigma (x)*y dx$

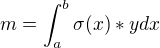
Meze pro půlkruh jsou dle mého od 0 do r
za y se dosadí $y= \sqrt{x^{2}-r^{2}}$
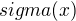ale co za $sigma (x)$ se má dosadit a za X mi nějak nevyplývá

Nebo se to má počítat podle jiných vzorců??

Předem moc děkuji

TomF · 15. 06. 2012 14:29

Zdravím,
pomocí integrálu nevím (jsem v prváku na střední), ale napadá mě řešení (podle mě jednodušší) a jde to používat i pro více ploch, než jen půlkruh. - Pappovy věty, určitě platí, když plochu "posunujeme" po kolmici. Bude ale oběm vytvořeného tělesa rotací plochy kolem osy roven součinu obsahu plochy a vzdálenosti, kterou urazí hmotný střed plochy? Asi ano, vzdálenější strana se posune vic a bližší méně...
Nechám teda půlkruh rotovat kolem "průměru kružnice" a vznikne koule, vzdálenost těžiště půlkruhu od "středu kružnice" označím x.

$(2\pi x)(\frac{1}{2}\pi r^{2})=\frac{4}{3}\pi r^{3}$

$x=\frac{4r}{3\pi }$

Rumburak

↑ zdenekm31:

Ahoj. Místo takovýchto speciálních vzorců je podle mne lepší pamatovat si obecnou rovnici

(1) $\int_{\Omega}\varrho(X)(X-T) \,\mathrm{d}X = 0$

charakterisující těžiště $T$ fyzikálního tělesa $\Omega$ , tj. bodové množiny, v níž je rozprostřena hmota o hustotě $\varrho(X)$ v bodě $X \in \Omega$ .
Úpravou rovnice (1) pak obdržíme

(2) $0 =\int_{\Omega}\varrho(X)(X-T) \,\mathrm{d}X = \int_{\Omega}\varrho(X)X \,\mathrm{d}X - \int_{\Omega}\varrho(X) T \,\mathrm{d}X = \int_{\Omega}\varrho(X)X \,\mathrm{d}X - m T$ ,

kde $m = \int_{\Omega}\varrho(X)\,\mathrm{d}X$ je hmotnost tělesa $\Omega$ . Z (2) pak smadno plyne

(3) $T = \frac{1}{m} \int_{\Omega}\varrho(X)X \,\mathrm{d}X$ .

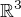Když $\Omega$ je oblastí v $\mathbb{R}^3$ , což je asi nejobvyklejší případ, pak $\varrho(X)$ je objemovou hustotou a v (1) - a tedy i v (2), (3) - je

$X = [x, y, z], T = [u, v, w] , \mathrm{d}X = \mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z$ ,

při čemž jde o trojrozměrné integrály, v nichž integrandem je trojrozměrná funkce, takže např. (1) se rozepíše po souřadnicích vektoru 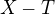$X-T$
do třech rovnic

$\int\!\!\!\int\!\!\!\int_{\Omega}\varrho(x, y, z)(x-u) \, \mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z = 0$ , $\int\!\!\!\int\!\!\!\int_{\Omega}\varrho(x, y, z)(y-v) \, \mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z = 0$ , $\int\!\!\!\int\!\!\!\int_{\Omega}\varrho(x, y, z)(z-w) \, \mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z = 0$ ,

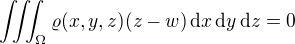čemuž bude odpovídat i tvar výpočtu (2) a jeho výsledku (3).

Analogicky by se postupovalo

- u rovinných obrazců ( $\varrho(X)$ by byla plošnou hustotou , integrály dvourozměrné z dvourozměrných funkcí) ,
- u obrazců na plochách v prostoru ( $\varrho(X)$ by byla plošnou hustotou , integrály plošné 1. druhu z trojrozměrných funkcí) ,
- u rovinných či prostorových křivek (když by se hledalo např. těžiště spirály) - jak v této situaci interpretovat $\varrho(X)$ a (1), (2) , (3) ,
si jistě už budeš umět sám doplnit.

zdenekm31 · 15. 06. 2012 15:27

Děkuji za návod na trojné integrály, ale potřebuju v jednoduchých to spočítat...

Měl jsem to napsat rovnou, omlouvám se

Rumburak

↑ zdenekm31:

Nešlo mi o to dávat návod na trojné integrály, ale snažil jsem se reagovat na podněty

zdenekm31 napsal(a):
...

Základní vzorce mam z více zdrojů, ale na žádném se mi neshodují, tak abych je mohl použít a byl si jist že je to správně,

...

ale co za $sigma (x)$ se má dosadit a za X mi nějak nevyplývá

Nebo se to má počítat podle jiných vzorců??
...

Takže se podívejme na půlkruh $\Omega = \{[x, y] \in \mathbb{R}^2 ; y > 0 \wedge x^2 + y^2 < r^2 \}$ o poloměru $r>0$ .
Plošnou hustotu bývá zvykem značit 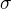$\sigma$ , takže podle toho, co jsem napsal předešle, bude

$m = \int_{\Omega}\sigma(X)\,\,\mathrm{d}X = \int \!\!\int_{\Omega} \sigma(x,y)\,\,\mathrm{d}x\, \mathrm{d}y = \int_{-r}^r\int_0^{\sqrt{r^2-x^2}} \sigma(x, y)\,\,\mathrm{d}y\, \mathrm{d}x$

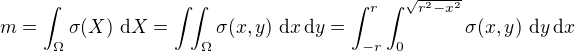
a podobně pro souřadnice těžiště

$u = \frac{1}{m} \int \!\!\int_{\Omega} \sigma(x,y)\,x\,\,\mathrm{d}x\, \mathrm{d}y = \frac{1}{m} \int_{-r}^r\int_0^{\sqrt{r^2-x^2}} \sigma(x, y)\,x\,\,\mathrm{d}y\, \mathrm{d}x$ ,

$v = \frac{1}{m} \int \!\!\int_{\Omega} \sigma(x,y)\,y\,\,\mathrm{d}x\, \mathrm{d}y = \frac{1}{m} \int_{-r}^r\int_0^{\sqrt{r^2-x^2}} \sigma(x, y)\,y\,\,\mathrm{d}y\, \mathrm{d}x$ .

Dál se ale nedostaneme, dokud nebudeme mít podrobnou znalost funkce $\sigma(x,y)$ . Váš učitel patrně vyšel z nějakých dílčích znalostí o této funkci
a dostal se ve výpočtu o něco dál - k jednorozměrným integrálům, které vám nadiktoval - s tím, že je dopočítáte. Proto jsi patrně nanašel shodu
"s jinými zdroji".

Abych mohl posoudit, zda vzorce, které uvádíš, jsou správně, musel bych o funkci $\sigma(x,y)$ vědět to, co váš učitel. Prozatím se mi to nezdá už kvůli těm
mezím a, b v integrálech. Jak souvisejí s půlkruhem ? Každopádně i 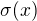$\sigma(x)$ je stále ještě příliš obecné, než aby bylo možno "Tvé" integrály spočítat.

Doporučuji zkontrolovat správnost zadání, například i to, zda má jít skutečně o půlkruh a ne třeba o oblouk kružnice a pod.

zdenekm31 · 15. 06. 2012 16:57

No tyto vzorce na těžiště nám byli nadiktovány a následně sme pomocí nich počítali těžiště u jiné oblasti. Jiné nám neuváděli na výpočet těžiště, tudíž sem předpokldal, jak vidím mylně, že těmi vzorce jdou spočítat všechna těžiště.

Jedná se stoprocentně o výpočet těžiště půlkruhu.

Rumburak

Můžeme ještě probrat speciální případ, kdy celý půlkruh je zhotoven z homogenního materiálu, takže ve všech jeho bodech je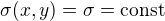
$\sigma(x,y) = \sigma = \text{const}$ . Potom tuto konstantu můžeme vytknout z integrálů a dostaneme

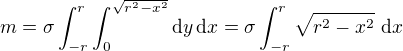$m = \sigma \int_{-r}^r\int_0^{\sqrt{r^2-x^2}} \mathrm{d}y\, \mathrm{d}x = \sigma \int_{-r}^r \sqrt{r^2-x^2}\,\, \mathrm{d}x$ , kde poslední integrál je roven obsahu půlkruhu,

$u = \frac{\sigma}{m} \int_{-r}^r\int_0^{\sqrt{r^2-x^2}}x\,\,\mathrm{d}y\, \mathrm{d}x = \frac{\sigma}{m} \int_{-r}^r x\, \sqrt{r^2-x^2}\,\, \mathrm{d}x = 0$ (integrujeme lichou funkci),

$v = \frac{\sigma}{m} \int_{-r}^r\int_0^{\sqrt{r^2-x^2}} y\,\,\mathrm{d}y\, \mathrm{d}x = \frac{\sigma}{m} \int_{-r}^r\frac{1}{2}\left(\sqrt{r^2-x^2}\right)^2\mathrm{d}x = ...$ , což dopočítat není těžké.

Ze vzorců, které uvádíš, i ten 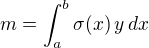$m = \int_{a}^{b}\sigma (x)\,y \,dx$ budí nedůvěru, protože výraz vpravo závisí na y-ové souřadnici,
tudíž to nemůže být hmotnost půlkruhu, kterou pro výpočet těžiště potřebujeme. Ony vzorce tedy mají jiný význam, než jaký
očekáváme, v tom bude ten zakopaný pes. Zkus toto přesně zjisti, tedy jaký význam mají meze integrálů, výrazy v integrandech
a integrační proměnné a co mají znamenat čísla S(x), S(y) a m.