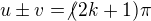Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 06. 2012 09:09
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Goniometrické rovnice
Dobrý den, pomůžete mi prosím s tímto příkladem? Vůbec nevím, kde mám začít. Díky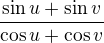
Offline
- (téma jako vyřešené označil(a) terezkaaaaa5)
#3 17. 06. 2012 09:55 — Editoval terezkaaaaa5 (17. 06. 2012 09:58)
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Goniometrické rovnice
↑ cyrano52:
Tak mi vzniklo 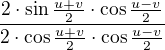 . A z toho vznikne
. A z toho vznikne 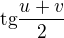 . Je to správně?
. Je to správně?
Offline
#4 17. 06. 2012 09:59
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Goniometrické rovnice
Akorát ještě potřebuji pomoct s definičním oborem. díky za pomoc.
Offline
#5 17. 06. 2012 09:59
- cyrano52

- Místo: Frýdek-Místek
- Příspěvky: 705
- Škola: VŠB-TUO Ekonomická fakulta
- Pozice: student
- Reputace: 29
Re: Goniometrické rovnice
↑ terezkaaaaa5:
Ano, jestli se dá udělat ještě něco dál poradí kolegové :)
Největší bohatství je vzdělání - R. Kiyosaki
Offline
#6 17. 06. 2012 10:10
- cyrano52

- Místo: Frýdek-Místek
- Příspěvky: 705
- Škola: VŠB-TUO Ekonomická fakulta
- Pozice: student
- Reputace: 29
Re: Goniometrické rovnice
↑ terezkaaaaa5:
Definičním oborem si nejsem úplně jistý, takže radši počkám na kolegy, promiň :)
Největší bohatství je vzdělání - R. Kiyosaki
Offline
#9 17. 06. 2012 10:27 — Editoval cyrano52 (17. 06. 2012 10:38)
- cyrano52

- Místo: Frýdek-Místek
- Příspěvky: 705
- Škola: VŠB-TUO Ekonomická fakulta
- Pozice: student
- Reputace: 29
Re: Goniometrické rovnice
Hm, uvidíme, co řeknou ostatní, já bych to spíše viděl na: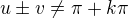
EDIT:// Wolfrámek říká, že je správně to s periodou 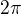 , ale teda nevím proč :(
, ale teda nevím proč :(
Největší bohatství je vzdělání - R. Kiyosaki
Offline
#10 17. 06. 2012 10:40
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Goniometrické rovnice
↑ cyrano52:
Doufám, že mi (nám) to někdo osvětlí. 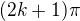 mi nedává smysl.
mi nedává smysl.
Offline
#11 17. 06. 2012 11:37
Re: Goniometrické rovnice
↑ cyrano52: Tady je ta zatoulaná dvojka:
Argument  nesmí být roven
nesmí být roven 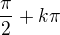 . To v našem případě znamená:
. To v našem případě znamená: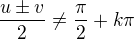 , což po vynásobení 2 jest:
, což po vynásobení 2 jest: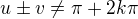
Offline
#12 17. 06. 2012 11:43
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Goniometrické rovnice
↑ Sulfan:
A je to tedy to samé co 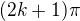 ?
?
Offline