Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 06. 2012 17:29
Příjmačky na VŠE 2008
Zdravím,
připravuji se na příjmačky na VŠE. a projíždím si zadání z roku 2008. Příklady 1-10 jsem dal v pohodě, ale s těmi za více bodů nemohu ani hnout. Pokud mi nějak poradíte či nakopnete budu rád.
Výsledky: 11B, 12D, 13C, 14A, 15D
Přestože hned 11) jsem našel tady -> http://forum.matweb.cz/viewtopic.php?pid=59702#p59702
Ale nechápu to dosazení, myslel jsem jsem že a=x na druhou - 3x
Díky moc všem za pomoc.
Offline
- (téma jako vyřešené označil(a) jelena)
#4 05. 06. 2012 18:10
Re: Příjmačky na VŠE 2008
↑ marnes:
Jóo už to vidim, jsem hloupý, omlouvám se :)
↑ zdenek1:
Omlouvám se, tohle mi uniklo.
Offline
#6 13. 06. 2012 21:58
Re: Příjmačky na VŠE 2008
Děkuju :)
Mám problém s principem příklad§ viz níže. Chápu první krok odstranění abs. hodnot, ale dále postup nechápu. Mohl by ho někdo nastínit? Díky moc
http://forum.matweb.cz/viewtopic.php?pid=123104#p123104 G1 1. příklad
http://forum.matweb.cz/viewtopic.php?pid=121869#p121869 E2 2. příklad
http://forum.matweb.cz/viewtopic.php?pid=121869#p121869 E3 2. příklad
Offline
#10 14. 06. 2012 23:00
Re: Příjmačky na VŠE 2008
Vždycky když si přečtu odpověď tak si přijdu o něco hloupější. Nic méně, pořád je tam spousta příkladů, u kterých si nejsem jist.
![kopírovat do textarea $1) z=(-1+i) [(-1+i)^{2}]^{16}\\
2) z=(-1+i) (i^{2}-2i+1)^{16}\\
3) z=(-1+i) (-2^{16}i^{16})$](/mathtex/6a/6aaffa7f528bb4bc4d82777b2239bb44.gif)
Je to tak? Co dále? Dočetl jsem se že se to dá řešit přes Moivreovu větu, ale o té jsem ve škole neslyšel a tady jsem to moc nepochopil, který způsob je lepší?
Offline
#13 15. 06. 2012 12:23
- cyrano52

- Místo: Frýdek-Místek
- Příspěvky: 705
- Škola: VŠB-TUO Ekonomická fakulta
- Pozice: student
- Reputace: 29
Re: Příjmačky na VŠE 2008
↑ veve3:
Ahoj, protože hledáš imaginární část komplexního čísla, které je definováno jako: , kde
, kde 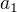 je reálná část a
je reálná část a  je imaginární část. Proto je správná odpověď C.
je imaginární část. Proto je správná odpověď C.
Největší bohatství je vzdělání - R. Kiyosaki
Offline
#14 15. 06. 2012 12:48
Re: Příjmačky na VŠE 2008

Řešil jsem to následujícím způsobem:
1) bod ta leží v půlce vektoru BC 
2) Udělám vektor který bude procházet body ta a A
3) 
Což je jasně špatně.. mám chybu ve výpočtu nebo v postupu, ještě mě napadlo to řešit přes pod T, který je 
↑↑ cyrano:
díky, toho jsem si měl všimnout ;)
Offline
#17 17. 06. 2012 12:00
Re: Příjmačky na VŠE 2008
↑ zdenek1:
http://forum.matweb.cz/viewtopic.php?pid=122279#p122279
6. Příklad
Proč jsi u cosinu neudělal

a zvolil jsi jiné řešení? Díky
Offline
#18 17. 06. 2012 12:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Příjmačky na VŠE 2008
↑ veve3:
Zdravím,
nebylo by pohodlnější založit si samostatné téma na každý dotaz? Viz pravidla.
úloha s tečnou - stačí počítat vzdálenost bodu S od přímky x+2y-7=0 (dle vzorce).
proč kolega Zdeněk nepřepsal  na
na 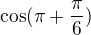 , protože umí z hlavy hodnotu
, protože umí z hlavy hodnotu  .
.
A už, prosím, zakládej si samostatné téma pro nový dotaz. Děkuji.
Offline
#20 17. 06. 2012 15:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Příjmačky na VŠE 2008
↑ veve3:
:-) a vytvářet si tak konkurenci v oboru?
Ale mně je to jedno :) (skoro (c))
Vážně - pokud chceš přidávat k topicu, tak můžeš jednotlivé úlohy konzultovat v samostatných tématech, potom do jednoho seřadit zadání a odkazy na řešení a umístit jako jeden příspěvek do zvýrazněného tématu.
Offline
#22 17. 06. 2012 22:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Příjmačky na VŠE 2008
↑ veve3:
:-) to si jen tropím žerty u přiležitosti 5. výročí příprav na VŠE.
Samozřejmě kolegům také děkuji a Tobě přeji zdárné přijímačky.
Offline


 upravíme a položíme menší jak 7
upravíme a položíme menší jak 7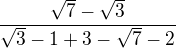
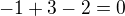 , to snad nepřekvapí. Zůstane
, to snad nepřekvapí. Zůstane




 Takže bych volil za A, kde je chyba?
Takže bych volil za A, kde je chyba?
