Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Plošný integrál 2.druhu, kontrola (TOTO TÉMA JE VYŘEŠENÉ)
#26 27. 06. 2012 16:50
Re: Plošný integrál 2.druhu, kontrola
↑↑ chipák:
a mohl bys to tady prosím konkrétně popsat, jak tu větu používáš a k jakému výsledku jsi se dostal? díky
Offline
#29 28. 06. 2012 10:56 — Editoval Rumburak (29. 06. 2012 11:42)
Re: Plošný integrál 2.druhu, kontrola
↑↑ chipák:
Ten vzorec z G.O. věty stačí si zapamatovat ve tvaru pro jednu obecnou složku jednotkového vektoru  vnější normály:
vnější normály:
(1)  ,
,
který se rovněž dá v mnoha případech použt. Nahradíme-li v něm funkci  funkcí
funkcí  , pak součtem přes
, pak součtem přes  , kde
, kde  je dimense prostoru
je dimense prostoru , v němž
, v němž  je uzavřenou omezenou oblastí s hranicí
je uzavřenou omezenou oblastí s hranicí  , vznikne známý vzorec s divergencí, z něhož pak zpětně vyplyne (1) jako jeho speciální
, vznikne známý vzorec s divergencí, z něhož pak zpětně vyplyne (1) jako jeho speciální
případ pro  ,
,  .
.
Vzorec (1) platí (za příslušných předpokladů) v prostorech  libovolné dimense. Například v "singulárním případě"
libovolné dimense. Například v "singulárním případě" 
máme Newtonův-Leibnizův vzorec
(2)  ,
,
takže pokud zde levou stranu při dobré vůli považujeme za jakýsi druh integrálu z funkce  přes orientovanou hranici
přes orientovanou hranici  intervalu
intervalu  s vnějšími
s vnějšími
jednotkovými normálovými vektory  , můžeme (2) považovat za variantu vzorce (1) . V tomto případě jde samozřejmě jen
, můžeme (2) považovat za variantu vzorce (1) . V tomto případě jde samozřejmě jen
o jakousi mnemotechnickou nadsázku.
Nutno ovšem si dát pozor na případ  , pokud jde o symboliku. Zatímco v
, pokud jde o symboliku. Zatímco v 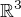 je
je  , kde pravou stranu můžeme
, kde pravou stranu můžeme
použít ve vzorci z G.O. věty v jeho obecném tvaru "s divergencí" , v 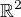 pak přesně analogický vztah mezi křivkovými integrály 1. a 2. typu obecně neplatí,
pak přesně analogický vztah mezi křivkovými integrály 1. a 2. typu obecně neplatí,
neboli
(3)  ,
,
takže v G.O. větě pro 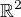 by použítí pravé strany z (3) by bylo chybou. Tato odlišnost
by použítí pravé strany z (3) by bylo chybou. Tato odlišnost 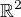 resp. odlišnost koncepce křivkového integrálu druhého typu od
resp. odlišnost koncepce křivkového integrálu druhého typu od
koncepce plošného integrálu druhého typu je vyjádřena Greenovou větou.
Offline
#30 29. 06. 2012 11:19 — Editoval Rumburak (29. 06. 2012 11:34)
Re: Plošný integrál 2.druhu, kontrola
↑↑ drabi:
Ještě jednou zdravím.
drabi napsal(a):
↑↑ Rumburak:
...
Jinak k té větě, na kterou jsi odkazoval, tak ty koeficienty A,B,C a jejich pronásobení s P,Q,R není nic jiného než skalární součin
Až tak jednoduché to není.
Je-li  zvolená parametrisace plochy (kde
zvolená parametrisace plochy (kde ![kopírovat do textarea $X=[x, y, z]$](/mathtex/e1/e1e9d2a932d1802efce6514262c38016.gif) je obecný bod prostoru),
je obecný bod prostoru),  jednotkový normálový vektor v bodě
jednotkový normálový vektor v bodě  a
a  funkce z té věty, pak spolehlivě můžeme říci pouze to, že existuje funkce
funkce z té věty, pak spolehlivě můžeme říci pouze to, že existuje funkce  taková, že
taková, že
 .
.
PŘÍKLAD. Vezměme rovinu popsanou rovnicí  , jejímž jednotkovým normálovým vektorem společným pro všechny její body je
, jejímž jednotkovým normálovým vektorem společným pro všechny její body je
(až na volbu znaménka)
 .
.
Parametrisujme ji rovnicemi  . Snadno zjistíme, že
. Snadno zjistíme, že  , takže
, takže
 .
.
Je zřejmé, že u složitější plochy se složitější její parametrisací můžeme očekávat i složitější funkci  . A odvodit její tvar pouze ze znalosti
. A odvodit její tvar pouze ze znalosti 
by se nám patrně nepodařilo. Proto je vhodnější používat přímo onu větu. Jako nejméně složité (a s minimálním risikem chyb) mi připadá každou ze tří částí
"souhrnného" plošného integrálu počítat separátně (případně i se zvlášní parametrisací výhodnou pro tu kterou část výpočtu), větu 2.3 pak používat v jejích
speciálních tvarech pro  resp.
resp.  resp.
resp.  a dílčí výsledky v závěru sečíst.
a dílčí výsledky v závěru sečíst.
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Plošný integrál 2.druhu, kontrola (TOTO TÉMA JE VYŘEŠENÉ)



 je vektorové pole
je vektorové pole 


