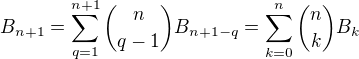Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Bellovo číslo, úprava sumy (TOTO TÉMA JE VYŘEŠENÉ)
#1 30. 06. 2012 15:39 — Editoval Andrejka3 (08. 07. 2012 14:02)
Bellovo číslo, úprava sumy
Dobrý den.
Počet všech ekvivalencí  prvkové množiny (n-té Bellovo číslo) mi vyšel
prvkové množiny (n-té Bellovo číslo) mi vyšel .
.
Mám ověřit, že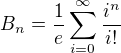 . (původně chyba - bylo n! ve jmenovateli.)
. (původně chyba - bylo n! ve jmenovateli.)
Příklad pochází z knížky Kapitoly z diskrétní matematiky, autorů Nešetřil, J. ; Matoušek, J., 4. vydání.
Cituji návod z knihy:
Návodu nerozumím. Mohl by mi, prosím, někdo ukázat, jak se to dělá?
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 30. 06. 2012 15:51
Re: Bellovo číslo, úprava sumy
Ahoj ↑ Andrejka3:,
Tvoj vzorec je dokazany v tomto prispevku
http://en.wikipedia.org/wiki/Dobinski%27s_formula
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 30. 06. 2012 16:00
Re: Bellovo číslo, úprava sumy
↑ vanok:
Díky.
V druhém vzorci ve wikipedii je drobný přepis, že? V levé sumě se sčítá od nuly?
Jinak, používají se tam věci, kterým nerozumím, ale jsem ráda, že vím, odkud to pochází.
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 06. 07. 2012 12:46 — Editoval vanok (09. 07. 2012 12:12)
Re: Bellovo číslo, úprava sumy
Ahoj,
Ten dokaz sa da urobit aj takto.
Vieme, ze 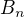 je pocet particii
je pocet particii  prvkovej mnoziny ( co je to iste ako pises "Počet všech ekvivalencí
prvkovej mnoziny ( co je to iste ako pises "Počet všech ekvivalencí  prvkové množiny")
prvkové množiny")
Nie je tazke ukazat ze mame tuto recurentnu relaciu:
Pre kazde 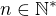 :
: 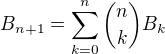
Dohodou polozme 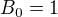
Teraz treba ukazat:
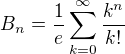
Ako prve treba overit, ze rada
 konverguje.
konverguje.To sa moze ukazat vdaka D'Alembert-ovmu testu.
Hladajme teraz, rekurecnu relaciu ktora plati pre

Toto znamena ze
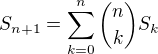
Takze pre
 a
a 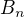 plati
platiKonkluzia:
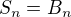 co je hladany vyrok.
co je hladany vyrok.Edit:oprava preklepov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 08. 07. 2012 10:37 — Editoval Andrejka3 (08. 07. 2012 16:55)
Re: Bellovo číslo, úprava sumy
↑ vanok:
Díky, moc hezky napsané. Ještě chvíli na zpracování...
V prvním příspěvku mám chybu. Mám dokázat, že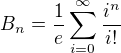
v sumě jsem psala ve jmenovateli chybně  .
.
Rekurentní vztah pro Bellova čísla je hezký a důkaz taky :)
Budu pokračovat dál. , chci dokázat, že
, chci dokázat, že pro
pro  a
a  .
.
Je  a
a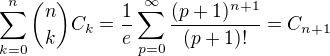 . Poslední rovnost mě mátla, protože jsem si neuvědomila, že
. Poslední rovnost mě mátla, protože jsem si neuvědomila, že  .
.
Ještě to projdu a pokud uvidím nějaké překlepy, pošlu opravu (nedivila bych se, když jsem měla chybně zadání).
Opravy?
Tak a je to :)
Díky a hezký den.
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 09. 07. 2012 12:19
Re: Bellovo číslo, úprava sumy
↑ Andrejka3:
Poznamka o tejto rovnosti:
Treba si uvedomit, ze ide len o nasobenie jednotkou 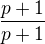
Inac som opravil, dufam vsetki male preklepy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Bellovo číslo, úprava sumy (TOTO TÉMA JE VYŘEŠENÉ)
 místo
místo 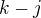 , nechte
, nechte  formálně probíhat do
formálně probíhat do  , a zaměňte pořadí sčítání podle
, a zaměňte pořadí sčítání podle 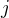 .
.
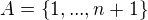 .
. jej podmnozinu
jej podmnozinu 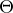 ktora ma
ktora ma  prvkov a osahuje
prvkov a osahuje  ; v tejto casti mame
; v tejto casti mame 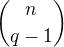 moznosti vybrat prvky rozne od
moznosti vybrat prvky rozne od 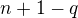 prvkov a da sa partitionovat
prvkov a da sa partitionovat 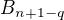 sposobmy.
sposobmy.