Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 12. 07. 2012 14:30
#6 12. 07. 2012 16:04
Re: Limita s e na a
↑ macher1:
Zdravím.
Toto ![kopírovat do textarea $[e^{a}]'=e^{a}.ln e$](/mathtex/43/43ea260f72aa9cbd4687522ee6c26072.gif) (kde navíc
(kde navíc 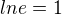 ) je samozřejmě pravda a vztah
) je samozřejmě pravda a vztah 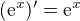 je celkem dobře znám.
je celkem dobře znám.
Kolega ↑ Sulfan: Tě chtěl upozornit na skutečnost, že 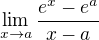 je speciálním případem (pro
je speciálním případem (pro 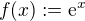 )
)
limity 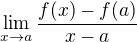 , kterou (pokud existuje) značíme
, kterou (pokud existuje) značíme 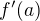 a nazývéme derivací funkce
a nazývéme derivací funkce  v bodě
v bodě  .
.
Viz definice derivace funkce jedné proměnné.
Offline

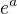 . Mne ale vychádza výsledok
. Mne ale vychádza výsledok 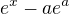 . Postupoval som tak že som použil L'Hospitalovo pravidlo. Poradí niekto čo s tým? Ďakujem.
. Postupoval som tak že som použil L'Hospitalovo pravidlo. Poradí niekto čo s tým? Ďakujem.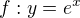 v bodě a.
v bodě a.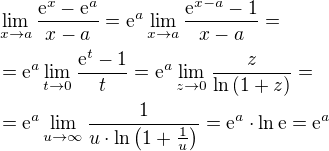 prípadne ak je
prípadne ak je 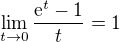 známa tak možno posledný riadok vynechať
známa tak možno posledný riadok vynechať