Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 07. 2012 22:19
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Algebraická čísla - dotaz
Zdravím.
Algebraická čísla jsou taková čísla x, pro které existuje polynom s celočíselnými koeficienty P takový, že P(x) = 0. Dočetl jsem se též o jedné vlastnosti algebraických čísel - tvoří těleso - tj. součet, rozdíl, součin i podíl dvou algebraických čísel je též algebraické číslo. Tak jsem si začal hrát a řekl si - ok, vezmu nějaká dvě algebraická čísla, sečtu je a dostanu též algebraické číslo a k tomu pak budu hledat příslušnou rovnici s celočíselnými koeficienty. U těch "hezčích čísel", kde není moc odmocnin apod. to není příliš těžké. Např. pro číslo 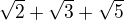 je příslušná rovnice "jenom" 8. stupně a vypadá takto:
je příslušná rovnice "jenom" 8. stupně a vypadá takto:  Zjistil jsem to tak, že jsem položil
Zjistil jsem to tak, že jsem položil  a pak jsem běžnými algebraickými úpravami a umocňováním na druhou postupně rovnici upravoval, dokud jsem se nezbavil všech odmocnin. Jenže třeba u čísla
a pak jsem běžnými algebraickými úpravami a umocňováním na druhou postupně rovnici upravoval, dokud jsem se nezbavil všech odmocnin. Jenže třeba u čísla  mám problém - těch odmocnin už je tam tolik, že ať už si je na levou a pravou stranu rozprostřu jakkoliv, tak po umocnění se celkový počet odmocnin (které vzájemně nejdou posčítat do jednoho členu) nezmenší. Tudíž mám problém s nalezením příslušné rovnice s celočíselnými koeficienty a nemůžu si tedy být jistý, zda se skutečně jedná o algebraické číslo. Poradíte mi? Díky za každou smysluplnou odpověď.
mám problém - těch odmocnin už je tam tolik, že ať už si je na levou a pravou stranu rozprostřu jakkoliv, tak po umocnění se celkový počet odmocnin (které vzájemně nejdou posčítat do jednoho členu) nezmenší. Tudíž mám problém s nalezením příslušné rovnice s celočíselnými koeficienty a nemůžu si tedy být jistý, zda se skutečně jedná o algebraické číslo. Poradíte mi? Díky za každou smysluplnou odpověď.
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#2 24. 07. 2012 10:19 — Editoval jarrro (24. 07. 2012 16:17)
Re: Algebraická čísla - dotaz
http://en.wikipedia.org/wiki/Resultant
http://mathworld.wolfram.com/Resultant.html
toto som vygooglil neviem či pomôže
MATH IS THE BEST!!!
Offline
#3 24. 07. 2012 18:52
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Algebraická čísla - dotaz
↑ Anonymystik:
Ahoj, pěkná úloha. Zatím jsem se nezamýšlel nad postupem, ale pokud budu mít čas, určitě se tomuto problému budu věnovat.
Pozn.: Zajímavé bylo totéž zjistit třeba pro číslo ![kopírovat do textarea $x = \sqrt{2} + \sqrt[3]{3} + \sqrt[5]{5} + \sqrt[7]{7} + \sqrt[11]{11}$](/mathtex/bb/bb3ce977c8d36bbe19c43e7545227468.gif) . :-))
. :-))
"Máte úhel beta." "No to nemám."
Offline
#4 24. 07. 2012 20:46
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Algebraická čísla - dotaz
↑ Anonymystik:
Ahoj, zatím mě napadlo toto:
Pokud důkaz věty o uzavřenosti algebraických čísel, je konstruktivní, pak nabízí postup jak daný polynom sestrojit a lze tedy postupovat indukcí podle "složitosti" výrazu definujícího x.
Nicméně k Tvému konkrétnímu případu: Zabývejme se problémem, kdy (schematicky psáno)  . Zkoumejme hodnoty
. Zkoumejme hodnoty 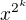 - každá tato hodnota je tvaru
- každá tato hodnota je tvaru  , kde
, kde 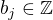 a
a  je součin některých (vždy však různých, případně žádných) čísel
je součin některých (vždy však různých, případně žádných) čísel  . Tedy pro dostatečně velké k dosáhneme toho, aby pro nějaké k0 bylo každé
. Tedy pro dostatečně velké k dosáhneme toho, aby pro nějaké k0 bylo každé  , které se v
, které se v 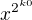 vyskytuje, přítomno i v jiném výrazu
vyskytuje, přítomno i v jiném výrazu 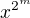 (tj. pro
(tj. pro 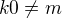 a
a 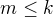 ) a aby k-1 nebylo menší než počet různých
) a aby k-1 nebylo menší než počet různých  ve všech těchto výrazech
ve všech těchto výrazech 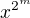 . Tím tedy získáme soustavu rovnic (výraz
. Tím tedy získáme soustavu rovnic (výraz 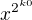 z této sousravy vynecháme) s neznámými
z této sousravy vynecháme) s neznámými  , které vyjádříme (zde je slabé místo / rovnice musí být nezávislé) pomocí x a dosadíme do výrazu definujícího
, které vyjádříme (zde je slabé místo / rovnice musí být nezávislé) pomocí x a dosadíme do výrazu definujícího 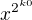 a tím získáme vztah pro x aniž bychom použili odmocniny - členy
a tím získáme vztah pro x aniž bychom použili odmocniny - členy  .
.
Takto jsem odvodil rovnici jejíž kořen je 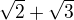 . Jednoduchost převládá nad obecnou ilustrací metody výše:
. Jednoduchost převládá nad obecnou ilustrací metody výše:
položíme 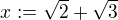 a tedy máme:
a tedy máme: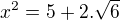
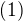
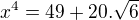
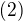
Tím jsme získali jednu rovnici (1) s jednou neznámou ( ), kterou vyřešíme a neznámé (resp. tu jedinou neznámou) dosadíme do druhé rovnice, tedy máme:
), kterou vyřešíme a neznámé (resp. tu jedinou neznámou) dosadíme do druhé rovnice, tedy máme: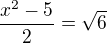 a po dosazení do druhé rovnice:
a po dosazení do druhé rovnice: a po úpravě
a po úpravě , což je hledaná rovnice.
, což je hledaná rovnice.
Otázka je, zda takto získáme polynom s minimálním stupněm, jehož kořen je dané číslo. Možná by bylo zajímavé, kdybys sem uvedl, jak metodou jsi tento příklad řešil ty, třeba půjde o jádro jiné obecné metody.
"Máte úhel beta." "No to nemám."
Offline
#5 24. 07. 2012 22:22 — Editoval vanok (24. 07. 2012 22:23)
Re: Algebraická čísla - dotaz
Mala poznamka:
Ako ↑ check_drummer: kolega ukazal, taketo metody na ukazanie ze sucet nejakych algebrickych cisiel je tiez algebricke cislo je pracne.
Ako poznamenal, kolega ↑ jarrro:, mozeme pouzit pojem resultanty
No vsak, treba vediet, ze Dedekind linearizoval tento problem vdaka pojmu MODUL (konecneho typu)
Cize mozeme znovu pochvalit kolegu ↑ Anonymystik:, ze dal do popredia tuto zaujimavu temu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 24. 07. 2012 22:58
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Algebraická čísla - dotaz
vanok napsal(a):
No vsak, treba vediet, ze Dedekind linearizoval tento problem vdaka pojmu MODUL (konecneho typu)
Ahoj, co prosím znamená Tvá poznámka, že daný problém byl linearizován? Děkuji.
"Máte úhel beta." "No to nemám."
Offline
#7 24. 07. 2012 23:05
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Algebraická čísla - dotaz
↑ vanok:
Ahoj, ještě jeden dotaz - z čeho prosím plyne, že koeficienty onoho "Resultantu" jsou v našem případě racionální čísla? To není zřejmé a je to podstatná vlastnost, kterou od tohoto polynomu v našem případě požadujeme. Děkuji
"Máte úhel beta." "No to nemám."
Offline
#8 25. 07. 2012 00:06 — Editoval vanok (25. 07. 2012 00:06)
Re: Algebraická čísla - dotaz
↑ check_drummer:
To sa lepsie vidi tu
http://fr.wikipedia.org/wiki/R%C3%A9sultant
kde je definovana resultanta ( alebo resultant???) dvoch polynomov ako determinant
Sylvestrer-ovej matice (co je equivalentne z definiciou v anglickej verzii)
↑ check_drummer:
Dedekind-ovu metodu najdes napriklad v Théorie algébrique des nombres, Pierre Samuel, éditeur Hermann
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 25. 07. 2012 00:59
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: Algebraická čísla - dotaz
Zdravím.
Chtěl bych všem poděkovat za hodnotné příspěvky - moc mi pomáháte s odpověďmi na mé otázky. Takže ještě jednou - díky.
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#10 25. 07. 2012 09:44 — Editoval jarrro (29. 07. 2012 15:39)
Re: Algebraická čísla - dotaz
čaute nedali by sa pri dôkaze, že v prípade polynómu ide o polynóm s racionálnymi koeficientami ak p, q sú také polynómy
ide o polynóm s racionálnymi koeficientami ak p, q sú také polynómy
nejako využiť vietove vzťahy? to ma len tak napadlo lebo sa tam objavujú súčty súčinov koreňov.
napr.http://www.wolframalpha.com/input/?i=Resultant%5B%28t-a%29*%28t-b%29%2C%28x-t-c%29*%28x-t-d%29%2Ct%5D&dataset=
že h má za korene súčty koreňov p a q je asi zrejmé keď sa p q napíšu ako súčiny koreňových činiteľov.
MATH IS THE BEST!!!
Offline
#11 25. 07. 2012 11:27 — Editoval vanok (25. 07. 2012 11:43)
Re: Algebraická čísla - dotaz
dobry den,
pridavam este jedno pdf kde sa vela najde o tejto teme.
Poznamka
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

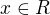
![kopírovat do textarea $A[x]$](/mathtex/ae/ae8e1ee6337b69ae3abeed8fcd4ed37a.gif) je A-modul konecneho typu
je A-modul konecneho typu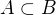 ,
,  a B je A-modul konecneho typu.
a B je A-modul konecneho typu.![kopírovat do textarea $A[x;y]$](/mathtex/04/047f2acc387baf43d012a5d682628c55.gif) , kde sa nachadzaju evidentne x+y; x-y, xy.
, kde sa nachadzaju evidentne x+y; x-y, xy.