Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Fyzika
- » Odvození rychlosti pohybu robotického ramena (s ryvem). (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 08. 2012 19:13 — Editoval jelena (28. 08. 2012 00:27)
Odvození rychlosti pohybu robotického ramena (s ryvem).
Zdravím,
při práci na mém projektu jsem se opět lehce zastavil na řešení jedné iracionální rovnice. Nemůžu s ní hnout. Zkoušel jsem ji řešit pomocí tužky a papíru, bohužel začala být tak rozsáhlá, že riziko numerické chyby bylo veliké. Zkoušel jsem ji zadat do Wolframu, bohužel v něm nejsem tak zdatný a pouhý příkaz Solve ji nedokázal vyřešit (možná by pomohlo zadání omezujíchc podmínek - bohužel nevím jak na to). "Klasicky bez přemýšlení" asi nejde rozumně vyřešit - ten správný fígl mě však zatím nenapadl.
Mé zadání je následující: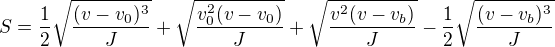
Tuto rovnici bych potřeboval vyřešit pro  (=zjistit vzoreček pro v). Jelikož se jedné o reálný problém, jsem schopen určit následující podmínky:
(=zjistit vzoreček pro v). Jelikož se jedné o reálný problém, jsem schopen určit následující podmínky:


Nevíte někdo jak na to? Budu vděčný za každou radu.
Nejsem si jistý kam tento problém zařadit - není to školní příklad a na SŠ se mi zdá poněkud obtížný.
Jelena: změna názvu tématu a přesun do Fyziky.
Offline
- (téma jako vyřešené označil(a) yaqwsx)
#2 25. 08. 2012 20:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
Zdravím,
ještě, než se začne řešit, - četla jsem Tvé téma ve Fyzice (o projektu), můžeš, prosím, upřesnit jednotlivá označení ve vzorci:  -rychlost,
-rychlost,  -moment setrvačnosti,
-moment setrvačnosti,  -? Mně se totiž nezdá tak na první pohled, zda sedí rozměrnost (jednotky) - kontroloval jsi?
-? Mně se totiž nezdá tak na první pohled, zda sedí rozměrnost (jednotky) - kontroloval jsi?
Wolfram by řešil asi pomoci takového zadání, ještě bych rovnou upravila, že celou rovnici vynásobím 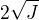 (zde opraveno), nepoužívat indexy, ale písmenka a, b apod., ale ani tak nevím, zda to zvládne.
(zde opraveno), nepoužívat indexy, ale písmenka a, b apod., ale ani tak nevím, zda to zvládne.
Snad někdo z kolegů by mohl zkusit zadat do svých programů, co mají, laskavě poprosím a děkuji.
Offline
#3 25. 08. 2012 21:26 — Editoval yaqwsx (25. 08. 2012 21:27)
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
Díky za reakci; jednotky jsou následující: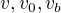 - rychlosti (cílová, počáteční, koncová) -
- rychlosti (cílová, počáteční, koncová) - 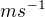
 - maximální ryv (CZ Wiki, EN Wiki) -
- maximální ryv (CZ Wiki, EN Wiki) -  - jedná se o veličinu charakterizující změnu zrychlení v čase.
- jedná se o veličinu charakterizující změnu zrychlení v čase.
K zadání: Mám zadaný maximální ryv  , maximální zrychlení
, maximální zrychlení  , cílovou rychlost
, cílovou rychlost  , počáteční rychlost
, počáteční rychlost 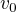 a koncovou rychlost
a koncovou rychlost  a dráhu (délku pohybu)
a dráhu (délku pohybu)  . Cílem je na zadané dráze dosáhnout rychlosti
. Cílem je na zadané dráze dosáhnout rychlosti  , přičemž při rozjezdu a brždění musí mít zrychlení sinový průběh s maximální amplitudou
, přičemž při rozjezdu a brždění musí mít zrychlení sinový průběh s maximální amplitudou  přičemž nesmí být překročen maximální ryv
přičemž nesmí být překročen maximální ryv  . Pokud však nastane situace, kdy je cílová rychlost
. Pokud však nastane situace, kdy je cílová rychlost  nastavena příliš vysoko a byl by překročen maximální ryv, nastupuje výše uvedený vztah, ze kterého by mělo být možno určit novou maximální rychlost
nastavena příliš vysoko a byl by překročen maximální ryv, nastupuje výše uvedený vztah, ze kterého by mělo být možno určit novou maximální rychlost  , které lze při daném omezení dosáhnout.
, které lze při daném omezení dosáhnout.
Od napsání prvního příspěvku jsem udělal drobný pokrok; rovnici jsem vynásobil  a toto násobení jsem zahrnul do
a toto násobení jsem zahrnul do  . Poté jsem ručně (s pomocí Wolframu) umocňoval. Stačilo umocnit 2× a dostal jsem se rovnost dvou dlouhých výrazů. Obsahují však 6. mocninu, tudíž (pokud jsem správně pochopil), nelze získat obecné řešení. Výsledek z Wolframu přiládám na konci. Pokud jsem neudělal chybu, tak přes tento vztah nevede cesta k obecnému řešení. To by nutně nemuselo znamenat problém - dalo by se to řešit interpolací hodnot z předpočítané tabulky (nemůžu si dovolit v reálném čase počítat řešení interační či jinou metodou).
. Poté jsem ručně (s pomocí Wolframu) umocňoval. Stačilo umocnit 2× a dostal jsem se rovnost dvou dlouhých výrazů. Obsahují však 6. mocninu, tudíž (pokud jsem správně pochopil), nelze získat obecné řešení. Výsledek z Wolframu přiládám na konci. Pokud jsem neudělal chybu, tak přes tento vztah nevede cesta k obecnému řešení. To by nutně nemuselo znamenat problém - dalo by se to řešit interpolací hodnot z předpočítané tabulky (nemůžu si dovolit v reálném čase počítat řešení interační či jinou metodou).
Byl bych však radši za obecné řešení. Jestli by tu byl zájem (neboli jestli by to vůbec někdo měl chuť číst), byl bych rád, kdybych tu uvedl můj kompletní úvahový postup a někdo další jej mohl zkontrolovat/přijít na nové řešení.
Výsledek z Wolframu (kde b= , o=
, o=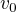 , x=
, x= )
)
Code:
{{x -> Root[
b^6 - 34 b^3 o^3 + o^6 + 8 b^3 S^2 + 8 o^3 S^2 +
16 S^4 + (2 b^5 + 48 b^2 o^2 + 62 b^3 o^2 + 206 b^2 o^3 +
2 o^5 + 8 b^2 S^2 + 8 o^2 S^2) #1 + (-b^4 - 16 b o -
64 b^2 o - 30 b^3 o - 160 b o^2 - 306 b^2 o^2 - 366 b o^3 -
o^4 - 8 b S^2 - 8 o S^2) #1^2 + (16 b + 16 b^2 - 2 b^3 +
16 o + 192 b o + 114 b^2 o + 112 o^2 + 498 b o^2 + 190 o^3 -
16 S^2) #1^3 + (-16 - 32 b - 15 b^2 - 128 o - 146 b o -
255 o^2) #1^4 + (16 + 16 b + 64 o) #1^5 &, 1]}, {x ->
Root[b^6 - 34 b^3 o^3 + o^6 + 8 b^3 S^2 + 8 o^3 S^2 +
16 S^4 + (2 b^5 + 48 b^2 o^2 + 62 b^3 o^2 + 206 b^2 o^3 +
2 o^5 + 8 b^2 S^2 + 8 o^2 S^2) #1 + (-b^4 - 16 b o -
64 b^2 o - 30 b^3 o - 160 b o^2 - 306 b^2 o^2 - 366 b o^3 -
o^4 - 8 b S^2 - 8 o S^2) #1^2 + (16 b + 16 b^2 - 2 b^3 +
16 o + 192 b o + 114 b^2 o + 112 o^2 + 498 b o^2 + 190 o^3 -
16 S^2) #1^3 + (-16 - 32 b - 15 b^2 - 128 o - 146 b o -
255 o^2) #1^4 + (16 + 16 b + 64 o) #1^5 &, 2]}, {x ->
Root[b^6 - 34 b^3 o^3 + o^6 + 8 b^3 S^2 + 8 o^3 S^2 +
16 S^4 + (2 b^5 + 48 b^2 o^2 + 62 b^3 o^2 + 206 b^2 o^3 +
2 o^5 + 8 b^2 S^2 + 8 o^2 S^2) #1 + (-b^4 - 16 b o -
64 b^2 o - 30 b^3 o - 160 b o^2 - 306 b^2 o^2 - 366 b o^3 -
o^4 - 8 b S^2 - 8 o S^2) #1^2 + (16 b + 16 b^2 - 2 b^3 +
16 o + 192 b o + 114 b^2 o + 112 o^2 + 498 b o^2 + 190 o^3 -
16 S^2) #1^3 + (-16 - 32 b - 15 b^2 - 128 o - 146 b o -
255 o^2) #1^4 + (16 + 16 b + 64 o) #1^5 &, 3]}, {x ->
Root[b^6 - 34 b^3 o^3 + o^6 + 8 b^3 S^2 + 8 o^3 S^2 +
16 S^4 + (2 b^5 + 48 b^2 o^2 + 62 b^3 o^2 + 206 b^2 o^3 +
2 o^5 + 8 b^2 S^2 + 8 o^2 S^2) #1 + (-b^4 - 16 b o -
64 b^2 o - 30 b^3 o - 160 b o^2 - 306 b^2 o^2 - 366 b o^3 -
o^4 - 8 b S^2 - 8 o S^2) #1^2 + (16 b + 16 b^2 - 2 b^3 +
16 o + 192 b o + 114 b^2 o + 112 o^2 + 498 b o^2 + 190 o^3 -
16 S^2) #1^3 + (-16 - 32 b - 15 b^2 - 128 o - 146 b o -
255 o^2) #1^4 + (16 + 16 b + 64 o) #1^5 &, 4]}, {x ->
Root[b^6 - 34 b^3 o^3 + o^6 + 8 b^3 S^2 + 8 o^3 S^2 +
16 S^4 + (2 b^5 + 48 b^2 o^2 + 62 b^3 o^2 + 206 b^2 o^3 +
2 o^5 + 8 b^2 S^2 + 8 o^2 S^2) #1 + (-b^4 - 16 b o -
64 b^2 o - 30 b^3 o - 160 b o^2 - 306 b^2 o^2 - 366 b o^3 -
o^4 - 8 b S^2 - 8 o S^2) #1^2 + (16 b + 16 b^2 - 2 b^3 +
16 o + 192 b o + 114 b^2 o + 112 o^2 + 498 b o^2 + 190 o^3 -
16 S^2) #1^3 + (-16 - 32 b - 15 b^2 - 128 o - 146 b o -
255 o^2) #1^4 + (16 + 16 b + 64 o) #1^5 &, 5]}}Offline
#4 25. 08. 2012 22:25
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
↑ yaqwsx:
děkuji za upřesnění, tedy představuji si, že pracuješ s rovnici 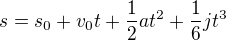 , překvapuje sice odvození, ke kterému jsi se dostal, ale určitě to máš podrobně ověřeno a promyšleno.
, překvapuje sice odvození, ke kterému jsi se dostal, ale určitě to máš podrobně ověřeno a promyšleno.
Bohužel pochybuji, že bych byla více užitečná, než případně přesunout téma do sekce Fyziky. Ať se podaří dořešit.
Offline
#5 26. 08. 2012 13:27
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
Pokusím se zde napsat celou mou úvahu od začátku do konce, abych si vše znovu v hlavě utřídil. Té si třeba někdo všimne něčeho, co mi uniklo. Mým cílem je popsat pohyb robotického ramene po úsečce. Cílem je minimalizovat (až odstranit) silové rázy a dosáhnout maximální dynamiky pohybu.
Mechanickou kontrukci, respektive její limity, charakterizuji maximální dosažitelným zrychlením  a maximálním ryvem (jerkem)
a maximálním ryvem (jerkem)  .
.
Abych minimalizoval silové rázy, jakákoliv změna rychlosti je relizována pomocí zrychlení se sinovým průběhem.
Zadání dostávám ve tvaru počáteční rychlosti 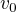 , požadované rychlost
, požadované rychlost  a požadované konečné (brzdné) rychlosti
a požadované konečné (brzdné) rychlosti  . Navíc dostávám počáteční a koncové souřadnice pohybu, z nichž určím délku úsečky, resp. dráhu
. Navíc dostávám počáteční a koncové souřadnice pohybu, z nichž určím délku úsečky, resp. dráhu  .
.
Základní úvaha
Můj pohyb by měl mít 3 části - rozjedz, pohyb konstatní rychlostí a brždění. Rozjezd trvá dobu  , bržedění trvá dobu
, bržedění trvá dobu  . Jelikož zrychlení má mít sinový průběh, bude jeho rovnice vypadat následovně:
. Jelikož zrychlení má mít sinový průběh, bude jeho rovnice vypadat následovně: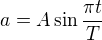
, kde  je aktuální čas. Pokud budu mít amlitudu zrychlení zápornou a perioda bude
je aktuální čas. Pokud budu mít amlitudu zrychlení zápornou a perioda bude  , platí tento průběh i pro brždění.
, platí tento průběh i pro brždění.
Pokud tento výraz zintegruji a patřičně doplním, získám vztah pro aktuální rychlost při rozjezdu v čase t:
respektive bržední: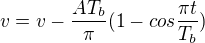
Pokud tento vztah znovu zintegruji, dostanu vztah pro dráhu uraženou za čas t při rozběhu:
resp. brždění:
Z výše uvedených vztahů můžu určit následující:
Pokud dosadím  , dostanu vztah pro celkovou ujetou dráhu S při rozjezdu:
, dostanu vztah pro celkovou ujetou dráhu S při rozjezdu:
resp. brždění:
Pokud do vzroce pro rychlost dosadím  , jsem schopen vyjádřit vztah pro periodu
, jsem schopen vyjádřit vztah pro periodu  , tak abych při pohybu dosáhl zadané rychlosti
, tak abych při pohybu dosáhl zadané rychlosti  , popř. brzdné rychlosti
, popř. brzdné rychlosti 
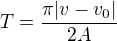

Tím je popsán nejjednodušší případ. Výsledek těchto vzorců jsem zanesl do grafu závisloti jednotlivých veličin na čase. V tomto grafu si lze povšimnout rozjezdu, pohybu konstatní rychlostí a brždění. Také jsem do něj zanesl okamžitý ryv 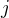 (pro další část tohoto příspěvku).
(pro další část tohoto příspěvku).
Kontrola vstupních dat
Vstupní data musím kontrolovat - může nastat situace, kdy nelze pomocí zadaného špičkového zrychlení  dosáhnout na dráze
dosáhnout na dráze  zadané rychlosti
zadané rychlosti  . Musím tedy zjistit, jakou maximální rychlostí se můžu na zadané dráze pohybovat. Úvaha je následující:
. Musím tedy zjistit, jakou maximální rychlostí se můžu na zadané dráze pohybovat. Úvaha je následující:
Pohyb na dráze lze popst následovně: , kde
, kde  je dráha uražená při rozjezdu a
je dráha uražená při rozjezdu a  je dráha uražená při brždění. Když celý vztah rozpeíšu dostanu následující:
je dráha uražená při brždění. Když celý vztah rozpeíšu dostanu následující:
Za  a
a  můžu dosadit výše uvedené vztahy (
můžu dosadit výše uvedené vztahy (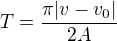 );
);
Po úpravě dostanu vzoreček pro maximální dosažitelnou rychlost v na dráze S:
Graf takového pohybu v závislosti na čase vypadá následovně:
Tuto úvahu mám již v praxi implementovanou a výsledky jsou více než uspokojivé. Jediný problém nastává u pohybů v malé rychlosti. Zatímco u pohybů ve velké rychlosti, kdy je potřeba mít dlouhou periodu  je maximální ryv malý, resp. menší než mechanické možnosti, tak u malých rychlostí je díky malé periodě
je maximální ryv malý, resp. menší než mechanické možnosti, tak u malých rychlostí je díky malé periodě  ryv obrovský - nad mechanické možnosti a je to znát. Je proto třeba zavést omezení ryvu.
ryv obrovský - nad mechanické možnosti a je to znát. Je proto třeba zavést omezení ryvu.
Omezení ryvu
Vztah pro aktuální ryv získám derivací vztahu pro zrychlení; tedy:
Je zřejmé, že maximální ryv nastává při  , tedy špičkový ryv
, tedy špičkový ryv  je roven:
je roven: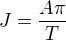
Díky tomuto vzorci lze zkonstuovat podmínku, zda-li není překročen maximální ryv. Pokud je překročen, je nutno určit nové hodnoty  a
a  .
.
To lze ze vztahu: dosazením
dosazením 
Dostanu vztah: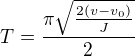
Z něj lze uričt i novou hodnotu pro  .
.
Toto je ta jednodušší situace.
Může však nastat situace, kdy i s nově dopočtenými omezenými hodnotami  a
a  nelze na dráze
nelze na dráze  dosáhnout zadané rychlosti
dosáhnout zadané rychlosti  a musím určit její novou hodnotu. Zde jsem si uvědomil, že jsem udělal chybu, rovnice v prvním příspěvku je špatně. Správná rovnice vypadá následovně.
a musím určit její novou hodnotu. Zde jsem si uvědomil, že jsem udělal chybu, rovnice v prvním příspěvku je špatně. Správná rovnice vypadá následovně.
Postupuji podobně jako v případě bez omezení ryvu - jen můžu mít rozdílnou hodnotu amlitudy zrychlení pro rozjezd a brždění - proto zavádím 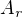 a
a  .
.

Kde: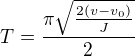



A když dosadím, dostanu vztah:
Každopádně i když je tato rovnice trochu jiná než ta původní, stále nemůžu najít její řešení. A ani mě nenapadl jiný způsob, jak zavést omezení  .
.
Doufá, že jsem vás tímto dlouhým příspěvkem neodradil. Bylo sice náročnější jej napsat, ale i kdyby nic, tak mi pomohl najít chybu v mém výpočtu.
Offline
#6 26. 08. 2012 23:37
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
↑ yaqwsx:
děkuji, ale bohužel nedovedu si jen tak na papíře představit si všechno. Jen takové dotazy k druhé (složitější) části:
a) co všechno v rovnici  (1) lze považovat za známou hodnotu? Jelikož mně se jeví vhodné uvažovat poměry
(1) lze považovat za známou hodnotu? Jelikož mně se jeví vhodné uvažovat poměry  (z dělení vztahů
(z dělení vztahů 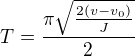 a
a  ) nebo vztahů
) nebo vztahů  a
a a pokud je možnost, v rovnici (1) jen nahradit jeden z časů (buď
a pokud je možnost, v rovnici (1) jen nahradit jeden z časů (buď  nebo
nebo  ).
).
Potom se mi zdá, že by vyjádření  mohlo být více reálné.
mohlo být více reálné.
b) rovnice (1)  popisuje celý průběh pohybu? Má tedy jen "zrychlující" a "zpomalující" úseky? Úsek konstantní rychlosti není? Na grafu ho vidím.
popisuje celý průběh pohybu? Má tedy jen "zrychlující" a "zpomalující" úseky? Úsek konstantní rychlosti není? Na grafu ho vidím.
Offline
#7 27. 08. 2012 09:10 — Editoval yaqwsx (27. 08. 2012 09:44)
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
Díky za reakci.
a) V této rovnici znám pouze  ,
, 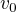 a
a  . S poměrem
. S poměrem  to vypadá na zajímavý nápad - prověřím ho.
to vypadá na zajímavý nápad - prověřím ho.
b)Ano, popisuje celý pohyb - není v něm konstatní složka - jelikož nejsem schopen zadané rychlosti (kterou bych se měl pohybovat) dosáhnout, tak se snažím pohybovat se co nejrychleji - tzn. zrychluji na nějakou špičkovou rychlost a ihned poté brzdím.
Offline
#8 27. 08. 2012 09:41
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
Zkusil jsem tedy nahradit jeden z časů výrazem  Rovnice začala vypadat slibně - vyskytoval se v ní pouze 1 výraz s odmocninou, který se dal vytknout - bohužel neznámá se v něm opět vyskytovala ve všech mocninách od 1 do 6.
Rovnice začala vypadat slibně - vyskytoval se v ní pouze 1 výraz s odmocninou, který se dal vytknout - bohužel neznámá se v něm opět vyskytovala ve všech mocninách od 1 do 6.
Podoba rovnice:
Stále přemýšlím nad nějakým zjdnodušením - zavedením nějakého omezení pro fyzikální model - čímž by se to celé mohlo zjednodušit, ale nic pořádného mě zatím nenapadlo.
Offline
#9 27. 08. 2012 23:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
↑ yaqwsx:
já se do tohoto problému nemohu dostat. Mám takové "překážky":
a) v rovnici  vůbec nevidím část pro ryv,
vůbec nevidím část pro ryv,
b) pokud je zrychlení podle harmonického průběhu (sinusoida), potom i rychlost podle harmonického průběhu ("cosinusoida") a to také v rovnici nevidím,
c) potom se mi zdá, že rychlost startovací a brzdicí spolu souvisí a zdá se, že celý průběh by šel rozdělit na dvě samostatné rovnice (ne součet  , který pořád bude špatně upravitelný). A v těch samostatných rovnicích se pokusit hledat uplatnění poměrů časů.
, který pořád bude špatně upravitelný). A v těch samostatných rovnicích se pokusit hledat uplatnění poměrů časů.
Raději to nechám tak, jedině ještě jednou nabídnu přesun do Fyziky a přejmenování na nějaký příhodnější název tématu. Snad se toho ujme někdo z odborných fyziků. Nebo konzultovat s vedoucím práce. Zdárné pokračování popřeji.
Offline
#10 27. 08. 2012 23:51 — Editoval yaqwsx (27. 08. 2012 23:52)
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
↑ jelena:
Opět děkuji za reakci. Přesun do fyziky asi bude nejlepší (předpokládám, že to zařídíte Vy - předem děkuji). Konzultovat bohužel nemám s kým - nejedná se o žádný školní projekt. Je to můj vlastní projekt - zatím na něm dělám sám.
a) Ta rovnice skutečně žádné omezení ryvu neobsahuje. Jednak se jedná o rovnici z úvahy, kdy ještě ryv neuvažuji a zároveň pokud z ní vyjde  dostatečně velké, tak ji ani ryv nelimituje (to v řízení ošetřím podmínkou).
dostatečně velké, tak ji ani ryv nelimituje (to v řízení ošetřím podmínkou).
b) Pokud je řeč o předchozí rovnici, tak v ní nemusím uvažovat okamžitý průběh rovnice (cosinusoidu), ale stačí mi uvažovat pouze celkovou uraženou dráhu a dosaženou rychlost.
Napadá mě paralela se vzorečkem dráhy rovnoměrně zrychleného pohybu  - také nepotřebuji znát průběh rychlosti (přímka).
- také nepotřebuji znát průběh rychlosti (přímka).
c)Tímto směrem se stále snažím ubírat, ale ne a ne to do sebe zapadnout. Pořád to nějak vzdoruje. Ale řešení tam asi někde bude.
Děkuji za podporu, snad se to poddá a výsledek zdárně najdu.
Offline
#11 28. 08. 2012 20:55
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
↑ jelena:
Možná ve vašich příspěvcích je zakódován klíč k řešení. Má úvaha o omezení ryvu asi není správná. Dnes jsem zkusil vyřešit rovnici Newtonovou metodou. Dostanu jeden reálný kořen, který projde zkouškou. Když však jeho výsledek dosadím do zbytku úvahy (tedy dosadím správné  ,
,  ,
,  a
a  ), tak pohyb probíhá špatně - maximální ryv sice sedí, ale urazím mnohem delší dráhu.
), tak pohyb probíhá špatně - maximální ryv sice sedí, ale urazím mnohem delší dráhu.
Svou úvahu budu muset nějak přehodnotit.
Offline
#12 28. 08. 2012 22:43
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
Jsem z toho jelen... Používám Newtonovu metody řešení výše uvedené rovnice. Pokud dosadím 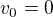 a
a  , tak výsledek je naprostá kravina. Pokud však dosadím např. za
, tak výsledek je naprostá kravina. Pokud však dosadím např. za  i 0.001, tak dostanu smysluplné hodnoty zatížené minimální chybou (několik setin procenta). Co mi uniká?
i 0.001, tak dostanu smysluplné hodnoty zatížené minimální chybou (několik setin procenta). Co mi uniká?
Offline
#13 29. 08. 2012 13:42
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
Už jsem zjistil, co mi uniká. Nastala drobná chybička při přepisu výstupu z Wolframu do C. Už jsem ji našel a opravil. Nyní hodnoty perfektně sedí (čímž vymizela i chyba - resp. je mnohem menší, než jsou mechanické limity)
Už vím, že rovnici jinak než numericky nevyřeším. Teď už si jenom vytvořím tabulku hodnot, abych mohl omezení ryvu provádět na ARMv7 procesoru. Doufám, že výsledek bude stát za to, když jsem s tím strávil tolik času.
Offline
#14 29. 08. 2012 16:49
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
↑ yaqwsx:
děkuji velice za zprávu, že to spěje k úspěchu.
Doufám, že výsledek bude stát za to, když jsem s tím strávil tolik času.
Ať tomu tak je. Zdravím.
Offline
#15 29. 08. 2012 17:15
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
První pokusy mám za sebou a hlásím, že to stálo za to. Pohyb je při malých rychlostech mnohem plynulejší. Děkuji za reakce, hodně mě popostrčily kupředu. Asi budu muset toto fórum navštěvovat častěji a zajisté ho i musím podpořit.
Rád bych se pochlubil i videem, ale myslím, že projekt zatím není ve stádiu, kdy je prezentovatelný (nyní mě čeká další - doufám poslední výzva - navazování přechodů mezi jednotlivými úseky (úsečkami, oblouky, atd) trajektorie).
Offline
#16 29. 08. 2012 23:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
↑ yaqwsx:
děkuji za podporu :-) Reakce kolegů určitě stoji za pochvalu, že se vzchopili i teď, v letním období, když je tak slunečno.
Rád bych se pochlubil i videem
tak až bude. Děkuji.
Offline
#17 29. 03. 2013 11:13
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
Vytahuji toto mé staré téma. Ještě jednou bych chtěl vám všem poděkovat za pomoc. Vaše odpovědi mě častokrát nakoply správným směrem.
Dotáhnout projekt do nějaké prezentovatelné podoby dalo ještě hodně práce, ale konečně se mi to povedlo. Na tomto odkazu si můžete prohlédnout demonstrační video, které jsem vytvořil pro účely obhajoby práce na Středoškolské odborné činnosti.
Offline
#19 29. 03. 2013 16:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Odvození rychlosti pohybu robotického ramena (s ryvem).
↑ yaqwsx:
Zdravím a děkuji velice za ukázku projektu, úspěšnou obhajobu přeji. Dovolila jsem si přidat odkaz do tématu "Místní ruční práce" (odkazy v 2. příspěvku) (lze přidat také i do Odborných - pokud máš zájem, zatím jsem se řídila, že to ruční provedení je moc pěkné :-), gratuluji), děkuji.
Offline
Stránky: 1
- Hlavní strana
- » Fyzika
- » Odvození rychlosti pohybu robotického ramena (s ryvem). (TOTO TÉMA JE VYŘEŠENÉ)


