Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 08. 2012 20:25
- check_drummer

- Příspěvky: 4634
- Reputace: 99
Komplexní body v reálné eukleidově rovině
Ahoj,
zamýšlel jsem nad tímto problémem:
Některé geometrické úlohy v Eukleidově rovině nemají vždy řešení (resp. množina řešení je prázdná), např. hledáme-li průnik kružnice a přímky, ne vždy existuje. Pokud tuto úlohu (a jí podobné) transformujeme do 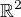 a využijeme metod analytické geometrie, pak v uvedeném případě řešíme soustavu, která "odpovídá" nějaké kvardatické rovnici. Pokud neznámé začneme chápat jako komplexní čísla (nikoli reálná), tak z tohoto pohledu lze říci, že kružnice má vždy s přímkou průnik, i když v některých případech jsou tyto souřadnice komplexní. Otázky, které se nabízí:
a využijeme metod analytické geometrie, pak v uvedeném případě řešíme soustavu, která "odpovídá" nějaké kvardatické rovnici. Pokud neznámé začneme chápat jako komplexní čísla (nikoli reálná), tak z tohoto pohledu lze říci, že kružnice má vždy s přímkou průnik, i když v některých případech jsou tyto souřadnice komplexní. Otázky, které se nabízí:
1) Lze si nějak "představit" tento ("komplexní") bod v eukleidově rovině, případně v nějakém prostoru, jehož je tato eukleidova rovina (obsahující danou kružnici a přímku) součástí? Teď nemám na mysli klasickou Gaussovu rovinu - ale nějaký prostor, aby se v něm opravdu nacházaly i ona kružnice a přímka.
2) Platí tvrzení, která platila pro "reálné" souřadnice průniku kružnice a přímky, i pro "komplexní" souřadnice? Abych byl konkrétní (a to se dostáváme k zadání úlohy), platí např. věta o mocnosti bodu ke kružnici? Tedy mějme bod P, přímku p procházející P a kružnici k. Označme A,B body průniku p a k (v případě, že p je tečna k, bude A=B). Potom věta o mocnosti bodu ke kružnici říká, že |PA|.|PB| je konstantní nezávisle na směru p. To platí (resp. má smysl) v případě, že p a k mají neprázdný průnik. (Tuto větu považujme za platnou a dokázanou.) Dle myšlenky výše lze zajistit, aby p a k měly průnik vždy (byť souřadnice bodů průniku A,B budou komplexní) a otázka zní, zda i pro tyto souřadnice zůstává uvedená věta v platnosti, tj. zda je stále |PA|.|PB| platné.
Bylo by zajímavé, zda např. také lze zobecněnou větu z bodu 2) dokázat i třeba nějakou algebraickou úvahou (bez "počítání"), ve které bychom např. využili jen platnost této věty pro "reálné" průniky. Pak by třeba bylo možné tuto úvahu zobecnit a použít i pro ostatní podobné věty.
"Máte úhel beta." "No to nemám."
Offline
#2 24. 08. 2012 21:44
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Komplexní body v reálné eukleidově rovině
1) Představit nevím, ale nestačí vzít prostě 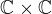 , kde rovnice přímky bude obecně
, kde rovnice přímky bude obecně  s komplexními koeficienty a,b,c a kde rovnice kružnice bude
s komplexními koeficienty a,b,c a kde rovnice kružnice bude 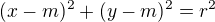 s komplexními m a n a r?
s komplexními m a n a r?
Jak by v tomto případě mohl vypadat důkaz:
Mám v rovině bod P (s reálnými souřadnicemi) a kružnici k (s reálným středem a poloměrem). Dále budu sestrojovat různé přímky p (s reálnými koeficienty) procházející bodem P. Pro přímku p si zavedu soustavu souřadnic 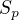 tak, že bod P bude v počátku soustavy souřadnic a přímka p bude totožná s osou x. Jednotku volím tak, aby rovnice kružnice k v soustavě
tak, že bod P bude v počátku soustavy souřadnic a přímka p bude totožná s osou x. Jednotku volím tak, aby rovnice kružnice k v soustavě 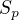 byla
byla 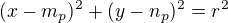 , všechny soustavy mají tedy stejné vzdálenosti (protože stejná kružnice má stejný poloměr). Protože se ve všech soustavách zachovávají vzdálenosti, zachovává se i vzdálenost mezi bodem P a středem kružnice, tedy
, všechny soustavy mají tedy stejné vzdálenosti (protože stejná kružnice má stejný poloměr). Protože se ve všech soustavách zachovávají vzdálenosti, zachovává se i vzdálenost mezi bodem P a středem kružnice, tedy 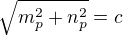 je nezávislé na přímce p.
je nezávislé na přímce p.
Rovnice přímky p v soustavě 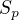 je
je  , takže průsečíky p a k v soustavě
, takže průsečíky p a k v soustavě 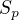 mají souřadnice
mají souřadnice  a
a 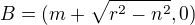 . Vzdálenosti |PA| a |PB| nezávisí na soustavě, v které je počítáme, takže pro přímku p je spočteme v soustavě
. Vzdálenosti |PA| a |PB| nezávisí na soustavě, v které je počítáme, takže pro přímku p je spočteme v soustavě 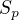 .
.
Vynásobením dostaneme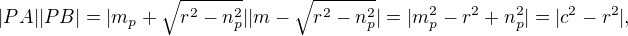
výsledek tedy nezávisí na tom, jakou přímku procházející bodem P vezmeme.
Nejsem si vůbec jistý, nakolik je to korektní, ale snad to k tématu aspoň trochu přispěje.
Offline
#3 29. 08. 2012 17:38
- check_drummer

- Příspěvky: 4634
- Reputace: 99
Re: Komplexní body v reálné eukleidově rovině
↑ Pavel Brožek:
Ahoj, děkuji za pěknou úvahu - za povšimnutí stojí zejména vhodná volba polohy přímky p.
Tedy obecně lze říci, že pokud ve výpočtech použijeme úpravy "společné" pro reálná i komplexní čísla, pak platí dané tvrzení i v komplexním oboru. (Ne vždy to však musí jít - např. pokud bychom v nějaké úvaze potřebovali porovnat dvě reálná čísla, pak tento postup v komplexním případě použít nejde.)
Druhá otázka týkající se "představení si" bodu s komplexními souřadnicemi v Eukleidově prostoru není pro další úvahy zas tak podstatná, spíš by mohla nějaké další úvahy usnadnit.
"Máte úhel beta." "No to nemám."
Offline