Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vektorove prostory (TOTO TÉMA JE VYŘEŠENÉ)
#1 18. 11. 2008 16:06
- Klara-Novotna

- Příspěvky: 33
- Reputace: 0
Vektorove prostory
Mějte vektorový prostor
P4: = { p(x)= a0 + a1x + a2xna2 + a3xna3 : a0, a1, a2, a3 náleží R}
Vypočítejte souřadnice vektorů
p(x) := 5xna3 + 3xna2 - 2x - 5 , q(x):= -xna3 + xna2 - 2
v bázi E : = {e1(x), e2(x), e3(x), e4(x)}, kde
e1(x) : = xna3 + x +1 ,
e2(x) : = xna2 - x,
e3(x) : = xna3 -x - 2,
e4(x) : = xna3 + xna2 -1
Offline
#2 18. 11. 2008 23:58
Re: Vektorove prostory
↑ Klara-Novotna:
Ukážu postup jen na jednom vektoru, třeba vektoru 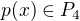 .
.
Souřadnice vektoru p(x) vzhledem k bázi  jsou takové prvky
jsou takové prvky 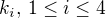 , pro které platí identita
, pro které platí identita
Odtud
Teď stačí porovnat koeficienty u příslušných mocnin x a dostaneš soustavu čtyř rovnic o čtyřech neznámých. Tu vyřešíš a máš hotovo. Analogicky pro vektor q(x).
Offline
#5 29. 03. 2009 12:21
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Vektorove prostory
↑ Coufal:Nejprve určíme vhodnou soustavu, vzhledem ke které to počítat. Její bázi bude tvořit zadaný vektor u, libovolný vektor na něj kolmý (např. 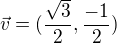 ) a třetí vektor musí být kolmý na oba, zvolme jej jako vektorový součin
) a třetí vektor musí být kolmý na oba, zvolme jej jako vektorový součin 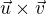 .
.
Matice zobrazení vůči této bázi je
1 0 0
0 cos(90°) -sin(90°)
0 sin(90°) cos(90°)
nyní stačí z ní vyrobit matici vůči kanonické bázi (řešilo se to nejen na fóru už mockrát).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#6 29. 03. 2009 20:30
Re: Vektorove prostory
1 0 0
0 cos(90°) -sin(90°)
0 sin(90°) cos(90°) je tedy rotace kolem osy "x" (Rx)
ale co rotace kolem osy "y" a "z"?
v sesite mam jeden priklad podobne ale s vektorem (1,1)... coz je 45° a reseni: Af= A -45° * Ay * A 45° to naprosto chapu...
ale "s vektorem u= (1/4, odmocnina 3 lomeno 4....) -> to jaky stupen? ° ?
Offline
#7 29. 03. 2009 21:12
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Vektorove prostory
Coufal napsal(a):
v sesite mam jeden priklad podobne ale s vektorem (1,1)... coz je 45° a reseni: Af= A -45° * Ay * A 45° to naprosto chapu...
To zase já naprosto nechápu :) Myšlenka těchto příkladů je v tom, že když chci spočítat souřadnice otočeného bodu, tak
1) jeho souřadnice převedu ze standardní báze do takové, ve které má otočení "hezkou" matici -- tedy za jeden prvek té báze určitě zvolím osu, kolem které otáčím, zbylé dva prvky souřadnice doplním tak, aby byly kolmé na sebe , kolmé na osu a byly jednotkové
2) v této bázi vynásobím souřadnice vektoru tou pěknou maticí zobrazení -- protože jsme si ji zvolili bázi šikovně (první prvek báze je kolineární s osou, další dva jsou na ni kolmé), bude mít matice otočení tvar
1 0 0
0 cos(x) -sin(x)
0 sin(x) cos(x)
3) souřadnice obrazu převedeme zpět do původní báze
První operaci odpovídalo násobení maticí přechodu A, druhé operaci násobení maticí otočení B a třetímu přechodu násobení maticí opačného přechodu, která je rovna 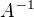 , což se díky kolmosti a jednotkovosti bázových vektorů rovná
, což se díky kolmosti a jednotkovosti bázových vektorů rovná 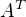 (tj. transponované matici A). Matice celého zobrazení je proto
(tj. transponované matici A). Matice celého zobrazení je proto 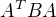 .
.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vektorove prostory (TOTO TÉMA JE VYŘEŠENÉ)