Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 11. 2008 22:14
- petulkacip
- Příspěvky: 38
- Reputace: 0
goniometrie
prosim o radu (vysvetleni) proc je v uvedenem priklade pouze k*pi a ne 2k*pi
nejak mi to v podstate unika u kazdeho prikladu...
prosim o radu jako pro nekoho, kdo tomu opravdu nerozumi
dekuju moc...
sin na druhou x - cos na druhou x = 0
-(cos na druhou x + sin na druhou x) = 0
-cos 2x=0
substituce: 2x=t
-cos t = pi\2 + k*pi (proc je tu jen k*pi a ne 2k*pi a jak to poznam i u dalsich pripadu - prosim o nejaky chytacek, ne odborny vyklad, to bych nepobrala
dekuju moc!!!
Offline
#2 18. 11. 2008 22:16
- petulkacip
- Příspěvky: 38
- Reputace: 0
Re: goniometrie
sel by vyse uvedeny priklad resit i rozkladem sin na druhou x - cos na druhou x = 0
sin na durhou x - 1 + sin na druhou x = 0
2sin na druhou x = 1
a jak by se potom postupovalo?
Offline
#3 18. 11. 2008 22:33
Re: goniometrie
Já se moc nevyznám v tom zadání příkladu. Co je vlastně původní zadání?  ?
?
Druhý řádek by měl asi plynout z toho prvního, je v něm ale chyba - má pak být  .
.
Nakonec z toho tedy plyne  , po substituci
, po substituci  .
.
(dále všude platí 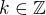 )
) se ve výsledku vyskytuje proto, protože se jedná o speciální případ, kdy se sinus či kosinus má rovnat nule. Vezmi si, že kdybychom měli třeba řešit
se ve výsledku vyskytuje proto, protože se jedná o speciální případ, kdy se sinus či kosinus má rovnat nule. Vezmi si, že kdybychom měli třeba řešit ,
,
tak dostaneme 2 řešení s příslušnou periodou, tj.
Když ale řešíme
tak řešení jsou
Protože ale od  po
po  je to právě
je to právě  a stejně tak od
a stejně tak od  po
po  je to taky
je to taky  , můžeme to zahrnout do jednoho výsledku
, můžeme to zahrnout do jednoho výsledku
Zkus si dosadit za k různá celá čísla a uvidíš, že výsledky ti pokryjí všechny možnosti.
Offline
#4 18. 11. 2008 22:44
- petulkacip
- Příspěvky: 38
- Reputace: 0
Re: goniometrie
takze pokazde, kdyz je sinus ci kosinus roven nule, tak pisu urcity vysledek = k*pi a ne 2*k*pi
ale pokud je to rovno nejake promenne, tak je to 2*k*pi??
Offline
#5 18. 11. 2008 22:46
- petulkacip
- Příspěvky: 38
- Reputace: 0
Re: goniometrie
ale vysledky se potom daji nejakym zpusobem slucovat?? a vynechavat ta dvojka?
Offline
#6 18. 11. 2008 22:58
Re: goniometrie
"pokud je rovno nějaké proměnné" - raději bych se vyvaroval termínu proměnná, jedná se o konstantu.
Ale ano, je to tak, že když je rovno nule, tak je tam jenom k*pi.
"ale vysledky se potom daji nejakym zpusobem slucovat?? a vynechavat ta dvojka?" - tak to bohužel nevím které výsledky máš teď na mysli.
Offline
#7 19. 11. 2008 10:21 — Editoval Cheop (19. 11. 2008 10:28)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: goniometrie
↑ petulkacip:
Zkusím Ti to vysvětlit takto:
Zadání: protože je to vlastně vzorec pro cos2x pak substituce 2x =t
protože je to vlastně vzorec pro cos2x pak substituce 2x =t vrátíme se k substituci a dostaneme:
vrátíme se k substituci a dostaneme:
Tady jasně vidíš proč je ta perioda 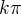 ,protože musíš celý výsledek vydělit 2 včetně původní periody
,protože musíš celý výsledek vydělit 2 včetně původní periody 
Nikdo není dokonalý
Offline
#8 19. 11. 2008 20:27
- petulkacip
- Příspěvky: 38
- Reputace: 0
Re: goniometrie
a dalo by se to nejakym zpusobem resit jako sin^2 x - cos^2 x =0; timhle vzorcem- sin^2x-1+sin^2x=0; 2sin^2 x = 1; dalo by se to nejak resit dal, nebo to je hovadina??
Offline
#9 20. 11. 2008 12:44
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: goniometrie
↑ petulkacip:
Jasně, že by se to dalo podle tohoto řešit.
Kořen 
Kořen  a z toho tedy můžeme psát:
a z toho tedy můžeme psát: a dostaneme stejný výsledek jako výše.
a dostaneme stejný výsledek jako výše.
Nikdo není dokonalý
Offline