Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 13. 01. 2011 20:00
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Konvexní množiny
Trivální odhad:
"Máte úhel beta." "No to nemám."
Offline
#3 13. 01. 2011 20:03 — Editoval check_drummer (14. 01. 2011 18:16)
#4 14. 01. 2011 17:31 — Editoval Olin (14. 01. 2011 17:35)
#5 14. 01. 2011 18:19
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Konvexní množiny
"Máte úhel beta." "No to nemám."
Offline
#6 16. 01. 2011 11:15 — Editoval check_drummer (05. 04. 2011 21:58)
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Konvexní množiny
Tak ještě jeden nápad:
"Máte úhel beta." "No to nemám."
Offline
#7 05. 04. 2011 20:30
Re: Konvexní množiny
↑ check_drummer:
Opět upozorňuji, že není zrovna vhodné označovat kontinuum jako  .
.
Protože se tato úloha spíš nehne, dám hint:
Offline
#8 12. 10. 2012 09:29
Re: Konvexní množiny
Offline
#9 13. 10. 2012 02:18
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Konvexní množiny
↑ Brano:
Ahoj, čím nám prosím Tvá konstrukce pomohla k vyřešení úlohy?
"Máte úhel beta." "No to nemám."
Offline
#10 14. 10. 2012 15:53
Re: Konvexní množiny
Tym, ze ju vyriesila :)
Offline
#12 14. 10. 2012 21:12
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Konvexní množiny
↑ Brano:
Děkuji. Využíváš tedy známého faktu, že 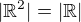 , že?
, že?
"Máte úhel beta." "No to nemám."
Offline
 . O tom, že to takto funguje i pro vyšší kardinály, již běžná hypotéza kontinua nehovoří, nazývá se to zobecněná hypotéza kontinua. Jinak jsou samozřejmě tyto odhady správně.
. O tom, že to takto funguje i pro vyšší kardinály, již běžná hypotéza kontinua nehovoří, nazývá se to zobecněná hypotéza kontinua. Jinak jsou samozřejmě tyto odhady správně.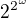 , tedy tolik, co všech podmnožin roviny.
, tedy tolik, co všech podmnožin roviny.


 je mnozina
je mnozina 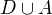 konvexna
konvexna je mnozina konvexnych podmnozin
je mnozina konvexnych podmnozin 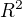 a
a 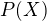 je potencna mnozina
je potencna mnozina  . Potom
. Potom
 pre
pre 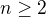 ale pre
ale pre 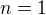 to neplati, lebo konvexne podmnoziny
to neplati, lebo konvexne podmnoziny  su intervaly a tych je
su intervaly a tych je 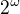 .
.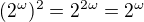 .
.