Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Záměna sumy a integrálu u funkční řady (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 10. 2012 14:01
Záměna sumy a integrálu u funkční řady
Dobrý den,
počítám následující příklad: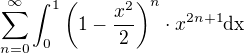
Tuším, že bych měl nějakým způsobem prohodit integrál a nekonečnou sumu, pokud bych uměl dokázat, že funkční řada je stejnoměrně konvergentní alespoň na 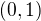 .
.
Ze srovnávacího kritéria jsem dostal, že by řada mohla stejnoměrně konvergovat, jelikož

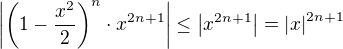
a řada  konverguje pro
konverguje pro  .
.
Můžu je přehodit a nekonečnou řadu sečíst - mohlo by to jít nějakým rozvojem, protože člen  vypadá podezřele, ale zase výraz neobsahuje faktoriál. Mohl by mi někdo poradit, jakým způsobem by se dala řada sečíst (jestli existuje třeba nějaký známý rozvoj)?
vypadá podezřele, ale zase výraz neobsahuje faktoriál. Mohl by mi někdo poradit, jakým způsobem by se dala řada sečíst (jestli existuje třeba nějaký známý rozvoj)?
Děkuji.
Offline
- (téma jako vyřešené označil(a) Sulfan)
#2 20. 10. 2012 17:19 — Editoval kaja.marik (20. 10. 2012 17:22)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Záměna sumy a integrálu u funkční řady
ja jsem dal substituci 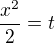 . Potom mi tam vyslo neco jako
. Potom mi tam vyslo neco jako 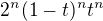 a pokud zasubstituuji tak, abych dostal
a pokud zasubstituuji tak, abych dostal  tak budu mit
tak budu mit 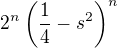 a to už by byla geometricka rada. Ale jenom jsem si to sketchnul na kousek novin, snad tam nemam chybu.
a to už by byla geometricka rada. Ale jenom jsem si to sketchnul na kousek novin, snad tam nemam chybu.
Offline
#3 20. 10. 2012 19:55 — Editoval Sulfan (20. 10. 2012 20:03)
Re: Záměna sumy a integrálu u funkční řady
Děkuji za odpověď, ale nějak nerozumím tomu, jak substituce proběhla. Pokud dosadím 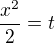 , tak mi vždy vyjde
, tak mi vždy vyjde  , kvůli tomu, že je v mocnině x výraz
, kvůli tomu, že je v mocnině x výraz  , kde dělám chybu?
, kde dělám chybu?
Edit: vyřešeno - x se vyhodí před sumu, tímto způsobem:
Offline
#4 20. 10. 2012 21:33 — Editoval kaja.marik (20. 10. 2012 21:36)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Záměna sumy a integrálu u funkční řady
↑ Sulfan:
jo aha, ten linearni posun do promenne s vlastne nebyl potreba. I kdyz ono se to pak vlastne stejne hodi pri vypoctu toho integralu.
K tomu x: ja jsem tu substituci delal v integralu a tam potom to x bylo soucasti vztahu mezi diferencialy.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Záměna sumy a integrálu u funkční řady (TOTO TÉMA JE VYŘEŠENÉ)