Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Tvorí množina vektorový podpriestor ? (TOTO TÉMA JE VYŘEŠENÉ)
#1 22. 10. 2012 23:55
- 010010

- Příspěvky: 82
Tvorí množina vektorový podpriestor ?
Dobrý deň.
Mám problém s pochopením riešenia príkladov podobných tomuto→
Uvažujme pod-množiny S a T vektorového podpriestoru R^3, ktoré sú určené takto. Máme rozhodnúť či množina S resp. T je lineárnym podpriestorom R^3.
S={(x,y,z); x^2 + y^2 =0}
T={(x,y,z); x^2 + z^2 =1}
Odpovede by mali byť S- ano T- nie
Pozeral som do skrípt, ale stále som neprišiel na to, ako mám takýto problém riešiť. Akým spôsobom. Definíciu podpriestoru a jeho podmienky poznám. Ale nikde tam nevidím nejak súvisloti, podľa čoho to presne určiť :/
Teda množiny S a T sú neprázdne.
A pokiaľ sa nemýlim aj keď vynásobím vektory skalárom, tak predpokladám že sú množiny uzavreté vzhľadom k operácii násobenia aj sčítania vektorov skalármi :/
Chcel by som vedieť teda nejaký slušný postup ako na to prídem aj v iných prípadoch, nie len v tomto.
Ďakujem za pomoc.
Offline
- (téma jako vyřešené označil(a) 010010)
#2 23. 10. 2012 00:03
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Tvorí množina vektorový podpriestor ?
http://msleziak.com/vyuka/2012/la/04vpry.pdf
Na kraji si vyhľadaj podpriestory. Sú tam v podstate dve podmienky, ktoré sa neskôr zlučujú do jednej. Podľa mňa stačí overiť tie.
Offline
#3 23. 10. 2012 00:16
- 010010

- Příspěvky: 82
Re: Tvorí množina vektorový podpriestor ?
Skriptá som už pozeral rôzne.
Vo všetkých sú zrejme tie isté podmienky, ak sa jedná o tú istú problematiku. Takže podmienky a kritéria poznám.
Ide mi skôr o tú jednoduchšiu interpretáciu problematiky.
Offline
#5 23. 10. 2012 20:16
Re: Tvorí množina vektorový podpriestor ?
Ahoj, píšeš:
010010 napsal(a):
Teda množiny S a T sú neprázdne.
A pokiaľ sa nemýlim aj keď vynásobím vektory skalárom, tak predpokladám že sú množiny uzavreté vzhľadom k operácii násobenia aj sčítania vektorov skalármi :/
Jak předpokládáš? To je právě to, co máš ověřit - uzavřenost na ty operace.
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 23. 10. 2012 20:22
- 010010

- Příspěvky: 82
Re: Tvorí množina vektorový podpriestor ?
Andrejka3 napsal(a):
Ahoj, píšeš:
010010 napsal(a):
Teda množiny S a T sú neprázdne.
A pokiaľ sa nemýlim aj keď vynásobím vektory skalárom, tak predpokladám že sú množiny uzavreté vzhľadom k operácii násobenia aj sčítania vektorov skalármi :/Jak předpokládáš? To je právě to, co máš ověřit - uzavřenost na ty operace.
Ja viem. Ale ja vidím všade, že ako keby všetky množiny boli uzavreté na operácie. A všetky nemôžu byť podpriestorom.
Známe množiny ako: R,I,Q,Z,N sú všetky uzavreté na operácie nás. a sčít.
Offline
#8 23. 10. 2012 20:37 — Editoval Andrejka3 (23. 10. 2012 20:39)
Re: Tvorí množina vektorový podpriestor ?
↑ 010010:
Píšeš:
Známe množiny ako: R,I,Q,Z,N sú všetky uzavreté na operácie nás. a sčít.
I není uzavřené, 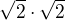 .
.
Edit: Je to jedno, nevím vlastně, jak si definujete I.
To je ale jiné tvrzení než že R,Q,Z,N jsou podprostorem  .
.
Vektorový prostor V nad tělesem T se píše takto: 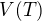 . Uzavřenost na násobení skalárem je tato podmínka:
. Uzavřenost na násobení skalárem je tato podmínka: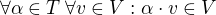 .
.
Všimni si, že tam jsou dvě množiny - jedna je  - množina vektorů,
- množina vektorů,  - množina skalárů.
- množina skalárů.
V našem případě, máme 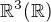 . To se implicitně předpokládá. Takže těleso je
. To se implicitně předpokládá. Takže těleso je  .
.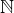 není podprostorem
není podprostorem  nad tělesem
nad tělesem  . Protože:
. Protože:
volme skalár 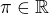 .
.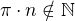 .
.
Podobně, 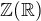 není podprostorem
není podprostorem 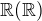 a podobně lze ukázat, že
a podobně lze ukázat, že
R,I,Q,Z,N nejsou podprostory  :
: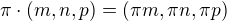 .
.
What does a drowning number theorist say?
'log log log log ...'
Offline
#9 23. 10. 2012 21:14 — Editoval Andrejka3 (24. 10. 2012 01:01)
Re: Tvorí množina vektorový podpriestor ?
Upřesním ten konec.
Andrejka3 napsal(a):
↑ 010010:
Podobně,není podprostorem
a podobně lze ukázat, že
R,I,Q,Z,N nejsou podprostory:
.
Chtěla jsem napsat.
... a lze ukázat, že 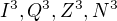 nejsou podprostory
nejsou podprostory  . Bez těch ''mocnin'' by to platilo triviálně, protože v prvé řadě musí být podprostor (jeho nosič) podmnožinou toho prostoru (jeho nosiče).
. Bez těch ''mocnin'' by to platilo triviálně, protože v prvé řadě musí být podprostor (jeho nosič) podmnožinou toho prostoru (jeho nosiče).
edit:
Ať nemám pocit, že jsem nic nevysvětlila, dám řešení pro množinu T={(x,y,z); x^2 + z^2 =1}
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Tvorí množina vektorový podpriestor ? (TOTO TÉMA JE VYŘEŠENÉ)
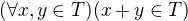
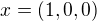
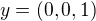
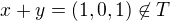 .
.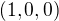 a
a 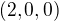 . Ten není v
. Ten není v