Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Součet mocninné řady (TOTO TÉMA JE VYŘEŠENÉ)
#1 27. 10. 2012 22:36
Součet mocninné řady
Dobrý den,
trápím se se součtem této mocninné řady:
kde !! je funkce dvojného faktoriálu (násobí se ob dva).
Určil jsem obor konvergence jako množinu všech reálných čísel a zkoušel jsem řadu nějakým způsobem sečíst, avšak bezúspěšně. Přepsal jsem si  , ale to nepomohlo. Dále jsem zkoušel hledat nějaký rozvoj funkce, který by se této řadě podobal, ale žádný jsem nenašel.
, ale to nepomohlo. Dále jsem zkoušel hledat nějaký rozvoj funkce, který by se této řadě podobal, ale žádný jsem nenašel.
Můžete mi poradit nějaký trik, jak řadu spočíst? Děkuji.
Offline
- (téma jako vyřešené označil(a) Sulfan)
#2 28. 10. 2012 01:37
- skoroakvarista

- Místo: Praha
- Příspěvky: 299
- Škola: FJFI ČVUT - ASI
- Pozice: Student
- Reputace: 20
Re: Součet mocninné řady
↑ Sulfan:
Zdravím, spíš než 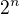 uprav
uprav  . Pomocí lehké substituce dostaneš to samé, co používáš při úpravě
. Pomocí lehké substituce dostaneš to samé, co používáš při úpravě 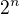 . Tak jsem dostal řadu do tvaru
. Tak jsem dostal řadu do tvaru  . To na první pohled nevypadá o moc lépe, ale pokud tuhle řadu zintegruješ, tak začne připomínat rozvoj sinu. Jen je potřeba se vhodnými úpravami zbavit
. To na první pohled nevypadá o moc lépe, ale pokud tuhle řadu zintegruješ, tak začne připomínat rozvoj sinu. Jen je potřeba se vhodnými úpravami zbavit  . Zkus si to sám, ale pro kontrolu dám i rozkouskovaný postup.
. Zkus si to sám, ale pro kontrolu dám i rozkouskovaný postup.
Použité úpravy, slovně:
Postup jedním směrem:
Druhý směr doplním ráno, pokud bude potřeba, teď už tu spím.
Offline
#4 28. 10. 2012 11:11
- skoroakvarista

- Místo: Praha
- Příspěvky: 299
- Škola: FJFI ČVUT - ASI
- Pozice: Student
- Reputace: 20
Re: Součet mocninné řady
↑ Sulfan:
Ještě doplním, že pro korektnost by se mělo ověřovat, jestli vůbec můžeme zaměnit pořadí sumy a integrálu. Ale pokud vím, tak je tenhle typ příkladů zadáván tak, aby ty záměny šly provést a ověření předpokladů není vyžadováno. Na to bývají vypečenější příklady...
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Součet mocninné řady (TOTO TÉMA JE VYŘEŠENÉ)
 . Velkým písmenem budu značit integrování.
. Velkým písmenem budu značit integrování. a vytknu
a vytknu  , potom
, potom 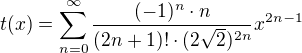 a
a  . Teď vhodně vynásobím
. Teď vhodně vynásobím  . A to už je ten slibovaný sinus
. A to už je ten slibovaný sinus 