Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Konvergence/ divergence řady (TOTO TÉMA JE VYŘEŠENÉ)
#1 28. 10. 2012 11:16
Konvergence/ divergence řady
Dobrý den,
snad už se na to někdo neptal přede mnou, hledala jsem a nenašla. Mám zjistit, jestli řada n!/(n^n), n --> oo, konverguje nebo diverguje. Tuším, že bude konvergovat, mohl byste mi prosím někdo poradit kritérium, kterým se to dá zjistit, ne samotné řešení? Nějak jsem se do toho zamotala... Už jsem zkoumala řadu n!/(5^n) pomocí podílového kritéria a ta diverguje. Bohužel se mi to tentokrát podílovým kritériem nějak nedaří.. Prosím o radu. Máme to sice jako nadstandardní úkol, ale chtěla bych to umět vyřešit.
Offline
- (téma jako vyřešené označil(a) nanny1)
#2 28. 10. 2012 11:28
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Konvergence/ divergence řady
↑ nanny1:
Použij limitní podílové kritérium, ať se zbavíš faktoriálu. Jinak ano, tato řada konverguje.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#3 28. 10. 2012 11:32
#4 28. 10. 2012 11:43 — Editoval nanny1 (28. 10. 2012 11:47)
Re: Konvergence/ divergence řady
↑ Aquabellla: Hm hm, zbavila jsem se faktoriálu, zbylo mi (n^n)/((n+1)^n). Mám teda napsat jmenovatel jako sumu - binomickou větu, pak můžu vytknout n^n, v čitateli mi zbyde 1 a jmenovatel jde k nekonečnu, limita je teda 0 a tudíž řada konverguje..? Nebo jsem vedle?
Edit: Teď na to koukám, to asi nepůjde, když jsem si to rozepsala, pokud vytknu n^n, zbyde mi v limitě 1 + samé nuly (jestli to vidím dobře..), takže 1/1 a to je asi špatně, když to konverguje. :(
Offline
#5 28. 10. 2012 12:08
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Konvergence/ divergence řady
↑ nanny1:
Dobrala jsi se ke správnému tvaru: 
Exponent se nám nehodí, přepíšeme si tvar na 

Dáme si substituci:  , takže se nám limita změní takto:
, takže se nám limita změní takto: 
Použijeme L'Hospitala:
Teď už stačí dosadit a vyjde konkrétní číslo menší jak jedna, takže původní suma konverguje.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#8 28. 10. 2012 14:59 — Editoval Mr.Pinker (28. 10. 2012 15:01)
Re: Konvergence/ divergence řady
jde to udělat i jinak .....![kopírovat do textarea $\sqrt[n]{\frac{n!}{n^n}}< 1$](/mathtex/35/35223a50ff1a2ff5b42a76411c934838.gif)
což po uprávě dává ![kopírovat do textarea $\sqrt[n]{n!}< n$](/mathtex/51/5151b976b1dcddc25e43d7e58c8fff55.gif)
což evidetně platí jelikož máš vztah ,že geometrický průměr je vždy menší roven průměru aritmetickému
což zní ![kopírovat do textarea $\sqrt[n]{n!}\le \frac{n+1}{2}$](/mathtex/3b/3b7d96b46aecb5f95b67e605d5fbc245.gif)
a jelikož pro n >1 platí
tak tvoje limita konverguje
vidím že než jsem se popral se sepsáním řešení je tu už další nu což snad ti pomůže i toto
Offline
#9 28. 10. 2012 17:13
Re: Konvergence/ divergence řady
↑ Mr.Pinker: Super, děkuju moc, pojem geometrický průměr jsem neznala, to je fakt užitečná věc. Jinak jestli se ještě můžu hloupě zeptat - v tom aritmetickém průměru je (n + 1)/2. Zrovna ta jednička je tam proč? Protože je to nejmenší možné n? Takhle se to dělá standardně? Omlouvám se, ještě jsem se s tím nesetkala a na Wiki to není.
Offline
#10 28. 10. 2012 17:29 — Editoval nanny1 (28. 10. 2012 17:49)
Re: Konvergence/ divergence řady
↑ Brano: Hmm.. Tak v tomhle se vůbec nechytám. Kde se vzalo (n - 1)! ještě tuším, ale jak jsi přišel na (n/2)^(n-1), to fakt nevidím. :( Zkoušela jsem limitní srovnávací kritérium a nikam jsem se nedostala, protože jsem tu limitu nedokázala nijak kloudně rozložit.
Upravila jsem výraz vytknutím n na (n-1)!/n^(n-1) a tu dvojku tam nějak nemůžu dostat. :(
Offline
#12 29. 10. 2012 09:27
#13 29. 10. 2012 09:51 — Editoval nanny1 (29. 10. 2012 10:15)
Re: Konvergence/ divergence řady
Ještě mě napadla jedna věc: U toho podílového limitního kritéria se výraz dal upravit na (n^n)/((n+1)^n), což se dá zapsat jako ((1/(1+(1/n)))^n, což je e^(-1) a to je taky menší než jedna. Jde to takhle taky udělat? :)
Offline
#14 29. 10. 2012 12:02 — Editoval Brano (29. 10. 2012 18:54)
Re: Konvergence/ divergence řady
↑ nanny1:
ano
↑ nanny1: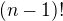 som tam dal, lebo sa mi to tak hodilo; potom
som tam dal, lebo sa mi to tak hodilo; potom .
.
no a ta AG nerovnost v tomto pripade hovori:![kopírovat do textarea $\sqrt[n-1]{(n-1)!}=\sqrt[n-1]{1\cdot 2\cdot ... \cdot (n-1)}\le\frac{1+2+...+(n-1)}{n-1}=\frac{n}{2}$](/mathtex/78/787c609496d8517648285b4f6ef7b60a.gif)
len taka poznamka, ze preco sa geometricky priemer vola geometricky:
poznas Euklidove vety? http://cs.wikipedia.org/wiki/Eukleidova_v%C4%9Bta
Zoberies si usecku 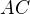 a na nej bod
a na nej bod  , tak ze
, tak ze 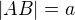 a
a  , urobis Talesovu kruznicu
, urobis Talesovu kruznicu  nad
nad 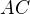 a kolmicu
a kolmicu  na
na 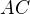 prechadzajucu bodom
prechadzajucu bodom  a oznacis bod
a oznacis bod  (tam su dva body, tak vyber jeden). Usecka
(tam su dva body, tak vyber jeden). Usecka  ktora ma z Euklidovej vety dlzku
ktora ma z Euklidovej vety dlzku  je isty sposob robenia priemeru
je isty sposob robenia priemeru 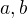 . Ocividne je dlzka
. Ocividne je dlzka  mensia, alebo rovna ako polomer kruznice
mensia, alebo rovna ako polomer kruznice  , cize
, cize  , pricom sa da lahko vsimnut, ze rovnost nastava iba ak
, pricom sa da lahko vsimnut, ze rovnost nastava iba ak 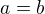 .
.
Tato nerovnost as potom da indukciou zovseobecnit na tento vztah: http://cs.wikipedia.org/wiki/Nerovnost_ … Fm%C4%9Bru
Pripadne si pozri anglicku verziu a najdes aj dokazy.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Konvergence/ divergence řady (TOTO TÉMA JE VYŘEŠENÉ)

 (zvladnes to dokazat z AG nerovnosti?)
(zvladnes to dokazat z AG nerovnosti?) a hotovo.
a hotovo.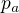 ted
ted 
 značí součet aritmetické řady takže dál je všechno jasné ne ?
značí součet aritmetické řady takže dál je všechno jasné ne ?