Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 10. 2012 17:15
vepsané a opsané útvary
2)Kouli je opsán rotační kužel, jehož výška se rovná šestinásobku poloměru koule r. V jakém poměru jsou povrchy obou těles?
1) Do rotačního kužele je vepsána koule, jejíž povrch se má k obsahu podstavy kužele jako 4:3. Vypočti
velikosti úhlů osového řezu rotačního kužele.
Prosím o výpočet
Offline
#2 29. 10. 2012 09:56
- marnes

- Příspěvky: 11227
Re: vepsané a opsané útvary
2)Kouli je opsán rotační kužel, jehož výška se rovná šestinásobku poloměru koule r. V jakém poměru jsou povrchy obou těles?
1) načrtni si osový řez dané situace, tj rovnoramenný trojúhelník ABC - AB základna - a do něj kružnici. Tato kružnice se dotýká základny v bodě K a ramene v bodě L a má střed S.
2) Trojúhelníky SLC a KBC jsou podobné
SC = 5r
SL = r
CK = 6r
a potřebujeme KB
z podobnosti plyne  kde CL vypočítáme z pravoúhlého trojúhelníku CSL.
kde CL vypočítáme z pravoúhlého trojúhelníku CSL.
Zbytek už snad zvládneš
Jo. A na začátku vás zdravím.
Offline
#3 29. 10. 2012 10:29
- marnes

- Příspěvky: 11227
Re: vepsané a opsané útvary
1) Do rotačního kužele je vepsána koule, jejíž povrch se má k obsahu podstavy kužele jako 4:3. Vypočti velikosti úhlů osového řezu rotačního kužele.
Opět náčrtek jako ve příkladě předešlém
Ze zadání plyne 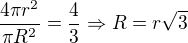
kde r je poloměr koule a R je poloměr podstavy
Dál si volím  , pak
, pak 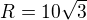
Počítám úhel u vrcholu C v trojúhelníku SCL 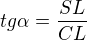
SL=r=10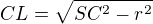
SC=v-10
dále platí 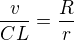 - vyjádříš v, zjistíš SC, zjistíš CL, vypočítáš alfa a pak už je to snadné
- vyjádříš v, zjistíš SC, zjistíš CL, vypočítáš alfa a pak už je to snadné
Třeba navrhne někdo něco jednoduššího
Jo. A na začátku vás zdravím.
Offline
#4 29. 10. 2012 11:34
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vepsané a opsané útvary
↑ marnes:
Zdravím,
2)Kouli je opsán rotační kužel, jehož výška se rovná šestinásobku poloměru koule r. V jakém poměru jsou povrchy obou těles?
zdá se, že mám o něco jednodušší postup pro (2), jelikož využívám jen podobnosti.
Už mne včera nebavilo opakovat pravidla a vyzývat k samostatnosti + použití tlačítka Hledat, tak to učiním dnes: ↑ Katerina6: (ne, že by to začalo bavit :-)
Offline
#5 30. 10. 2012 08:59 — Editoval Cheop (30. 10. 2012 10:43)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: vepsané a opsané útvary
↑ Katerina6:
Oba příklady jdou řešit pomocí analytické geometrie
Ukázka řešení př. 1)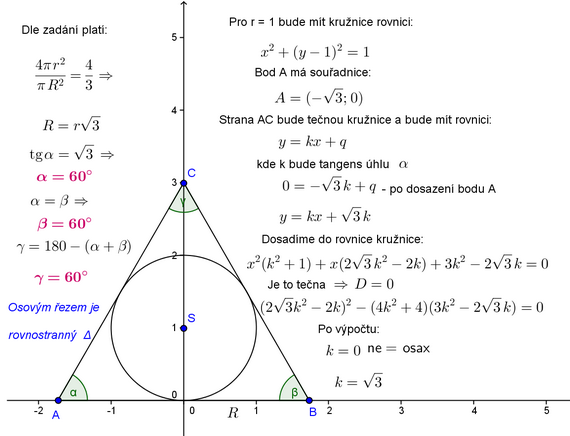
Nikdo není dokonalý
Offline
#6 30. 10. 2012 09:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vepsané a opsané útvary
Zdravím v tématu,
sleduji, že jsem přehodila číslování úloh a můj odkaz je pro úlohu (2). Opravila jsem ↑ v příspěvku 5: a přidala text úlohy.
Ještě přidám k (1)
1) Do rotačního kužele je vepsána koule, jejíž povrch se má k obsahu podstavy kužele jako 4:3. Vypočti
velikosti úhlů osového řezu rotačního kužele.
Zde je vhodné uvažovat, že střed kružnice vepsané leží na ose úhlu. Tedy pokud spojím bod v základně A se středem S, mám trojúhelník AOS (ve značení kolegy ↑ Cheop:), ve kterém je tangens polovičního úhlu při základně 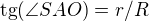 .
.
↑ Cheop: můj obdiv :-)
Kateřině to je ovšem srdečně jedno :-) pokud by se objevila, tak ať dá do pořádku témata, co založila.
Offline