Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 10. 2012 17:25 — Editoval vanok (31. 10. 2012 17:26)
pekna teorema o radoch
Dokazte tento vysledok
Nech 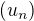 je divergentna rada zo striktne kladnymy clenmy.
je divergentna rada zo striktne kladnymy clenmy.
Oznacme 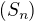 jej sumu radu
jej sumu radu  , potom rada
, potom rada je
je
konvergentna ak  ,
,
divergentna ak  .
.
A potom skuste ho aplikovat na dokaz nejakych klasickych viet,
o ktorych napisem tu http://forum.matweb.cz/viewtopic.php?pid=312503#p312503
v prispevku #132
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 01. 11. 2012 17:07
Re: pekna teorema o radoch
Pekna uloha. Najprv ako by to vyzralo v spojitom pripade.
Mozno, ze integralne kriterium poskytne ako dosledok vetu o radoch, len mne sa nepodarilo doladit detaily. Ale mozeme sa inspirovat tymto postupom a dokazat vysledok pre rady osobitne.
Offline
#3 01. 11. 2012 18:34 — Editoval vanok (02. 11. 2012 11:17)
Re: pekna teorema o radoch
Ahoj ↑ Brano:,
Dakujem, ze ta tento problem zaujal.
Dam este jeden dokaz, mozes to porovnat z tvojim.
Ak 
Ak
 , pouzijem Cauchy-ho kriterium a ukazem, ze
, pouzijem Cauchy-ho kriterium a ukazem, ze  ho nesplnuje.
ho nesplnuje.Co znamena, ze
 .
.Skutocne, mame
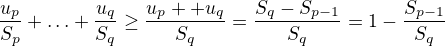
Pre dane
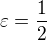 a pre
a pre  nech
nech  a
a  take ze
take ze 
Odtial, pre
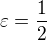 a p, q takto urcene
a p, q takto urcene 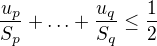 .
.A preto rada
 diverguje.
diverguje.Ak

vieme, ze rada
 , ca da ze
, ca da ze 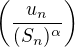 diverguje.
diverguje.KONIEC
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 01. 11. 2012 21:30
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: pekna teorema o radoch
↑ vanok:
Ahoj, můžeš prosím více odůvodnit platnost nerovnosti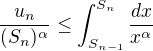
?
Děkuji
"Máte úhel beta." "No to nemám."
Offline
#5 01. 11. 2012 23:15 — Editoval Brano (01. 11. 2012 23:16)
Re: pekna teorema o radoch
↑ vanok:
Cize hovoris, ze aj pre 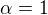 to diverguje? Skusal som to dokazat, len sa mi to nepodarilo.
to diverguje? Skusal som to dokazat, len sa mi to nepodarilo.
Este sa mi ten tvoj postup nejak nezda. Pre  , plati
, plati 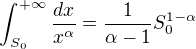 , co je pre
, co je pre  mensie ako prvy clen v tom rade ..
mensie ako prvy clen v tom rade ..  .
.
PS: Mne sa zda, ze plati plati opacna nerovnost a da sa pouzit na divergenciu toho radu.
Offline
#6 02. 11. 2012 00:20 — Editoval vanok (02. 11. 2012 01:10)
Re: pekna teorema o radoch
Ahoj ↑ check_drummer:,
Uvedom si ze 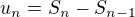 .
.
Z toho mas okamzite nerovnost co som napisal, vdaka teoreme strednej hodnoty integralu.
Ahoj Brano, zatial som dokazal vysledok pre 
Co sa tyka tvojej poznamky, porozmyslam o tom.
Pripad 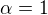 je zatial predcastne komentovat ... vsak zatial som tu nenapisal ziadny dokaz. ( A v dokaze skutocne uvidis ze v tom pripade rada diverguje.) Ked dokoncim co mam na praci napisem ten dokaz co som slubil... este troska trpezlivosti.
je zatial predcastne komentovat ... vsak zatial som tu nenapisal ziadny dokaz. ( A v dokaze skutocne uvidis ze v tom pripade rada diverguje.) Ked dokoncim co mam na praci napisem ten dokaz co som slubil... este troska trpezlivosti.
Zatial mozte mi napisat, ci je vam cast co som napisal jasna, alebo ukazat ci tam je nejaka chyba..
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 02. 11. 2012 01:36
Re: pekna teorema o radoch
↑ vanok:
Uz som si overil, ze to plati tak ako si napisal a uz vidim aj kde bol problem v mojej uvahe. Totizto 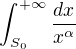 je sucet radu bez prveho clena - t.j. toho s indexom
je sucet radu bez prveho clena - t.j. toho s indexom 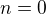 . Ked sa pripocita aj ten, tak dostaneme presne ten isty horny odhad sumy co vysiel aj mne.
. Ked sa pripocita aj ten, tak dostaneme presne ten isty horny odhad sumy co vysiel aj mne.
Offline
#8 02. 11. 2012 11:35 — Editoval vanok (03. 11. 2012 14:32)
Re: pekna teorema o radoch
Doplnil som moj dokaz, tak napiste ak mate otazky alebo poznamky ( chyba nie je vylucena, ale dufam ze su tam len preklepy a nic ine)
Tu http://forum.matweb.cz/viewtopic.php?pid=312503#p312503 v prispevku #132 som dal este jednu malu poznamku na jednoducje pouzitie tohto vysledku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 05. 11. 2012 16:07
Re: pekna teorema o radoch
Pokud v původním příspěvku značí výraz bez diakritiky
%--------
jej sumu radu 
%-------- -tý parciální součet, potom se mi vybavují tři jména, konkrétně Abel, Dini a Pringsheim s jejich větami o nekonečných řadách. Důkaz tvrzení výše (domnívám se elementárnější, než zde předvedené, ale detaily jsem nestudoval) je možno nalézt v Knoppově knize zde. Zajímavá je pak také věta Theorem 3 na straně 126 od E. Cesàra, jež je v úzké souvislosti s těmito výsledky. Ve slovenštině je možno tyto výsledky v ucelené a zajímavé podobě nalézt v knize Tibora Šaláta Nekonečné rady. V češtině máme, bohužel, málo takové literatury (snad Holendovy Řady).
-tý parciální součet, potom se mi vybavují tři jména, konkrétně Abel, Dini a Pringsheim s jejich větami o nekonečných řadách. Důkaz tvrzení výše (domnívám se elementárnější, než zde předvedené, ale detaily jsem nestudoval) je možno nalézt v Knoppově knize zde. Zajímavá je pak také věta Theorem 3 na straně 126 od E. Cesàra, jež je v úzké souvislosti s těmito výsledky. Ve slovenštině je možno tyto výsledky v ucelené a zajímavé podobě nalézt v knize Tibora Šaláta Nekonečné rady. V češtině máme, bohužel, málo takové literatury (snad Holendovy Řady).
Offline
#10 05. 11. 2012 17:30 — Editoval vanok (05. 11. 2012 17:59)
Re: pekna teorema o radoch
Pozdravujem ↑ Marian:,
Zial diakritiku na Cz a Sk nemam.
2 knihy o radoch od Knopp som konzultoval. Dokaz v nich je inac urobeny.
K Sk kniham je mi tiez prakticky nemozne sa dostat, ak su in line, tak sa rad poucim.
Zda sa mi, ze dokaz co som tu dal je dost elemetarny
Cesaro-va veta, je iste zaujimava, ale o suvise z danym problemom som zatial nerozmyslal.
Mozno tu napisem, o elementarnych vlasnostiach Cesaro- konvegencii radu k, inspirovanu z knihy od Hardy (divergent series)... No ale to je len projekt.
Mala poznamka: V mojej edicii thm od Cesaro je na str 129.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 ,
,  a
a  pre
pre  . Skumame konvergenciu integralu
. Skumame konvergenciu integralu  . Pouzijeme substituciu
. Pouzijeme substituciu  a dostaneme
a dostaneme  pre
pre 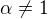 a
a 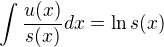 . Cize integral diverguje ak
. Cize integral diverguje ak 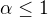 a konverguje ak
a konverguje ak  ,
, 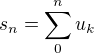 a
a  pre
pre 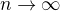 . Skumame konvergenciu radu
. Skumame konvergenciu radu 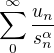 . Rad ocividne diverguje pre
. Rad ocividne diverguje pre 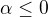 . Predpokladajme, ze
. Predpokladajme, ze  . Oznacme
. Oznacme 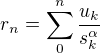 . Dokazme indukciou, ze
. Dokazme indukciou, ze  . Pre
. Pre 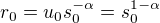 cize ok. Ak
cize ok. Ak  potom
potom  . Pre
. Pre  plati
plati  , teda rad diverguje. Teraz nech
, teda rad diverguje. Teraz nech 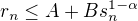 , pre vhodne
, pre vhodne 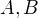 . Pozrime sa najprv na indukcny krok a zistime, ze staci aby platilo
. Pozrime sa najprv na indukcny krok a zistime, ze staci aby platilo 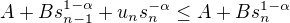 . Oznacme
. Oznacme  a
a 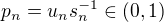 a teda
a teda  . Dosadme do nerovnice a dostaneme
. Dosadme do nerovnice a dostaneme  , po upravach
, po upravach ![kopírovat do textarea $B\left[(1-p_n)^{-\beta}-1\right]\le-p_n$](/mathtex/27/272729a6070bcc2c45aa2803b6682e33.gif) . Budeme potrebovat tuto nerovnost
. Budeme potrebovat tuto nerovnost  , pre
, pre 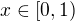 a
a 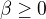 . Z nej mame, ze
. Z nej mame, ze 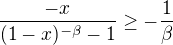 , takze staci zobrat
, takze staci zobrat 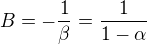 a
a  zvolime tak, aby nerovnost platila pre
zvolime tak, aby nerovnost platila pre 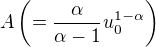 .
.