Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 10. 2012 21:39
Slovní úlohy (rovnice)
Zdravím, potřeboval bych pomoct s řešením těchto slovních úloh.
1) Vypočtěte obsah pravoúhlého trojúhelníku, jehož delší odvěsna je o 3cm kratší než přepona a o 3cm delší než kratší odvěsna.
2) Rameno rovnoramenného trojúhelníku měří 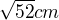 , jeho základna je o 2cm delší než k ní příslušná výška. Vypočtěte obsah tohoto trojúhelníku.¨
, jeho základna je o 2cm delší než k ní příslušná výška. Vypočtěte obsah tohoto trojúhelníku.¨
Díky za pomoc.
Offline
- (téma jako vyřešené označil(a) Yepy)
#2 31. 10. 2012 22:12
Re: Slovní úlohy (rovnice)
Ahoj,
1) to závisí na volbě přepony, tak můžeš řešit jen obecně: vyjádříš přeponu jako neznámou a odvěsny jako přepona-...
2)nejprve je třeba spočítat výšku: pomoví pythagorovy věty sestavíš kvadratickou rovnici s výškou jako neznámou +(a tady po vyřešení vyjde jeden kořen záporný, ten nechceme).
Neberme rozum do hrsti, mohli bychom zjistit, že je prázdná.
Offline
#3 01. 11. 2012 05:49
Re: Slovní úlohy (rovnice)
↑ TomF:
K př.1. To co píšeš není přeci pravda.
Máš trojúhelník, o kterém znáš 3 na sobě nezávislé údaje. (pravoúhlý, a dvě strany podmíněné stranou třetí)
Offline
#5 01. 11. 2012 19:33 — Editoval Vladislav97 (01. 11. 2012 20:19)
- Vladislav97

- Místo: Praha
- Příspěvky: 421
- Škola: Gymnázium
- Pozice: Student (Druhák)
- Reputace: 13
Re: Slovní úlohy (rovnice)
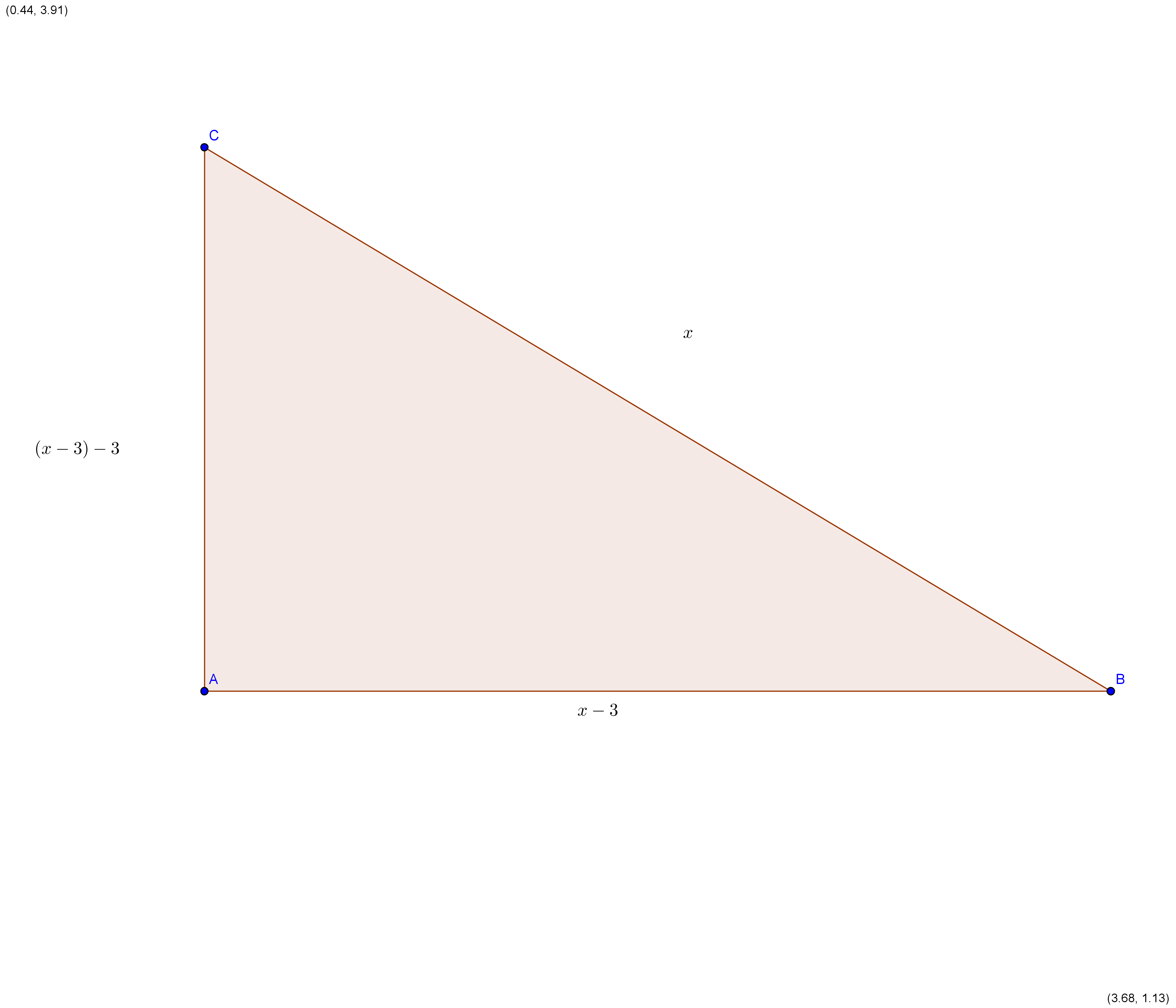
↑ Yepy: Ahoj, vzorec pro obsah trojúhelníka spočítáš tak, že vynásobíš délku základny s výškou a tento celý údaj vydělíš dvěma. Tady přikládám můj schématický obrázek:
Teď si tkus podle Pythagorovy věty dopočítat
 . Rozepíšu začátek:
. Rozepíšu začátek: 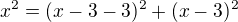
Offline
#6 01. 11. 2012 19:41
- Vladislav97

- Místo: Praha
- Příspěvky: 421
- Škola: Gymnázium
- Pozice: Student (Druhák)
- Reputace: 13
Re: Slovní úlohy (rovnice)
↑ Yepy: U dvojky se pokus narýsovat trojúhelník a vyznačit si co znáš. Opět prozradim, že tam využiješ Pythagorovy věty (ale ne pro celý trojúhelník, jenom pro nějakou část).
Offline
#8 01. 11. 2012 19:55 — Editoval Vladislav97 (03. 11. 2012 12:24)
- Vladislav97

- Místo: Praha
- Příspěvky: 421
- Škola: Gymnázium
- Pozice: Student (Druhák)
- Reputace: 13
Re: Slovní úlohy (rovnice)
Jak si z 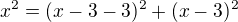 přišel na:
přišel na:
? kam ti zmizely mocniny? A 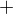 ti nějak zmizel...
ti nějak zmizel...
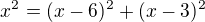 Zde by se ti hodilo použít vzorec:
Zde by se ti hodilo použít vzorec: 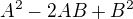 tedy:
tedy: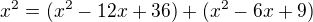
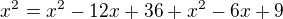 (A upravuj)
(A upravuj)
Jasné?
Za pár minutek tu už nebudu, tak pokud budeš potřebovat něco vědět, tak ti pomůžou ostatní, kteří budou moci. Popřípadně se tu objevim ještě. Zdar a hodně úspěchu v tématu.
Offline
#9 02. 11. 2012 06:03 — Editoval Honzc (02. 11. 2012 06:07)
Re: Slovní úlohy (rovnice)
↑ Yepy:
K příkladu 1.
Pokud jste ještě nebrali kvadratickou rovnici, ale brali jste úpravu výrazů, pak se dá úloha spočítat takto:
Označíme prostřední délku strany (jedné odvěsny) 
Další dvě strany tj. druhá odvěsna bude mít délku  a přepona délku
a přepona délku 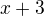
Pak podle Pythagorovy věty bude platit: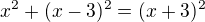
Upravíme (umocníme dvojčleny)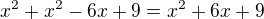
Odečteme sečteme a máme: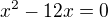
Vytkneme:
A teď už pouze zapřemýšlíme. Kdy je součin dvou čísel roven nule?
Odpověď: když alespoň jedno z nich je rovno nule.
Tak tedy 1.  - to ovšem nevyhovuje, protože se jedná o délku úsečky a ta nulová být nemůže
- to ovšem nevyhovuje, protože se jedná o délku úsečky a ta nulová být nemůže
2.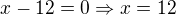 , a to je řešení (je to ta delší z odvěsen)
, a to je řešení (je to ta delší z odvěsen)
Druhou odvěsnu spočítáme jako 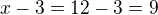
Máš tedy vypočítané délky obou odvěsen a teď už jenom dosadíš do vzorečku 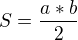
Jenom taková poznámka:
Pravoúhlemu trojúhelníku, který má všechny délky stran tvořeny přirozenými čísly (u nás 9,12,15) se říká pythagorejský trojúhelník.
Offline
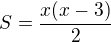
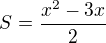
![kopírovat do textarea $S=\frac{(x-3)*[(x-3)-3]}{2}$](/mathtex/db/db99ad2019c613ebfa00483f37a0ee17.gif)