Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Obor konvergence řady (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 11. 2012 20:52
Obor konvergence řady
Zdravím,
hledám obor konvergence následující mocninné řady:
kde je -1 umocněná na dolní celou část přirozeného indexu n. Zde mi selhává "klasický" výpočet oboru konvergence za pomoci napříklady limity podílu dvou po sobě jdoucích členů. Uvážil jsem, že bych nějakým způsobem mohl odhadnout dolní celou část jako:
ale to bohužel nevedlo k cíli, protože umocňuji mínus jedničku a mezi jejími mocninami by tento vztah už neplatil.
Máte nápad, jak vyšetřit obor konvergence této řady?
Děkuji za odpověď.
Offline
- (téma jako vyřešené označil(a) Sulfan)
#2 05. 11. 2012 21:10 — Editoval Pavel Brožek (05. 11. 2012 21:13)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Obor konvergence řady
↑ Sulfan:
Zkus si to rozdělit na tři případy  ,
,  a
a  . Zvládneš některý z nich?
. Zvládneš některý z nich?
Offline
#3 05. 11. 2012 21:22 — Editoval Sulfan (05. 11. 2012 21:24)
Re: Obor konvergence řady
↑ Pavel Brožek:
Pro  limita v plus nekonečnu neexistuje, tudíž množina
limita v plus nekonečnu neexistuje, tudíž množina  nebude v oboru konvergence.
nebude v oboru konvergence.
Pro  konverguje absolutně například dle limitního podílového kritéria, tudíž
konverguje absolutně například dle limitního podílového kritéria, tudíž  je podmnožinou oboru konvergence.
je podmnožinou oboru konvergence.
Ale pro  si stále nevím rady. Nevíš, jak bych mohl pokračovat? Díky. :)
si stále nevím rady. Nevíš, jak bych mohl pokračovat? Díky. :)
Offline
#7 09. 11. 2012 18:16
Re: Obor konvergence řady
Omlouvám se, že jsem dlouho neodpověděl, ale už je mi to jasné, děkuji ↑ Rumburak:.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Obor konvergence řady (TOTO TÉMA JE VYŘEŠENÉ)
 ,
, 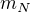 je největší přirozené číslo splňující nerovnost
je největší přirozené číslo splňující nerovnost  , tj.
, tj. 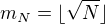
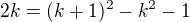 , pro
, pro 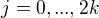 je tedy
je tedy 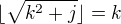 ,
, 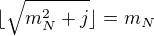 .
.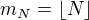 ?
? , už jsem opravil.
, už jsem opravil.