Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 11. 2012 19:42 — Editoval Pavel Brožek (10. 11. 2012 21:22)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Dimenze prostoru komutujících matic
Mějme  danou matici typu
danou matici typu 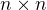 nad tělesem
nad tělesem  . Jaká je dimenze vektorového prostoru matic, které s
. Jaká je dimenze vektorového prostoru matic, které s  komutují?
komutují?
Ve speciálním případě, kdy matice  má různá vlastní čísla, je hledaná dimenze rovna n, jak jsem ukázal zde. Jak je to ale v obecném případě?
má různá vlastní čísla, je hledaná dimenze rovna n, jak jsem ukázal zde. Jak je to ale v obecném případě?
Edit: Já řešení neznám, připadá mi to ale jako zajímavý problém, který bychom společnými silami mohli vyřešit.
Offline
#2 10. 11. 2012 20:16
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Dimenze prostoru komutujících matic
↑ Pavel Brožek:
Ahoj, k té původní úloze, kterou uvádíš, jsem napsal pár otázek.
"Máte úhel beta." "No to nemám."
Offline
#3 10. 11. 2012 21:18
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dimenze prostoru komutujících matic
Matice  se dá rozložit na Jordanův rozklad
se dá rozložit na Jordanův rozklad 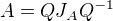 (
( je regulární matice složená ze zobecněných vlastních vektorů,
je regulární matice složená ze zobecněných vlastních vektorů,  je matice s Jordanovými bloky). Hledáme matice
je matice s Jordanovými bloky). Hledáme matice  , pro které platí
, pro které platí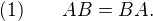
To přepíšu pomocí Jordanova rozkladu a upravím.
Pro každou matici  tedy existuje matice
tedy existuje matice 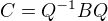 , která splňuje
, která splňuje
Najdeme-li všechny matice  splňující (2), snadno pomocí nich vyjádříme všechny matice splňující (1) jako
splňující (2), snadno pomocí nich vyjádříme všechny matice splňující (1) jako  .
.
Stačí tedy problém vyřešit pro speciální matice – blokově diagonální matice složené z Jordanových bloků. Když nám někdo zadá matici, která není v takovém tvaru, snadno převedeme problém na tento jednodušší.
Offline
#4 10. 11. 2012 21:54
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Dimenze prostoru komutujících matic
↑ Pavel Brožek:
A bude pak přechodem mezi 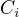 (některé
(některé  podle Tvého značení) a
podle Tvého značení) a  (jim odpovídající
(jim odpovídající  podle Tvého značení) zachována nezávislost? Tedy - budou matice
podle Tvého značení) zachována nezávislost? Tedy - budou matice 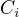 lineárně nezávislé, právě když budou matice
lineárně nezávislé, právě když budou matice  lineárně nezávislé? (Otázka je důležitá pro to, abychom mohli rozhodnout o dimenzi jen pomocí matic
lineárně nezávislé? (Otázka je důležitá pro to, abychom mohli rozhodnout o dimenzi jen pomocí matic  .)
.)
"Máte úhel beta." "No to nemám."
Offline
#5 10. 11. 2012 22:12
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dimenze prostoru komutujících matic
Dále v tomto tématu předpokládejme, že  je blokově diagonální s Jordanovy bloky. Počet různých vlastních čísel matice
je blokově diagonální s Jordanovy bloky. Počet různých vlastních čísel matice  si označme
si označme  a vlastní čísla označme
a vlastní čísla označme  , kde
, kde 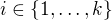 .
.
Pro vlastní číslo  matice
matice  si označme
si označme 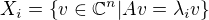 (
(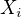 je podprostor vektorů s vlastním číslem
je podprostor vektorů s vlastním číslem  ).
).
Nechť  . Pak platí
. Pak platí 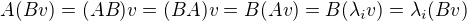 , vektor
, vektor 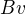 je tedy také vlastním vektorem matice A s vlastním číslem
je tedy také vlastním vektorem matice A s vlastním číslem  , tedy
, tedy 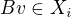 . Podprostor
. Podprostor 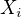 je tedy invariantní při působení B. To znamená, že B musí být blokově diagonální, kde bloky odpovídají jednotlivým invariantním podprostorům
je tedy invariantní při působení B. To znamená, že B musí být blokově diagonální, kde bloky odpovídají jednotlivým invariantním podprostorům 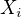 .
.
Matice  a
a  se tedy násobí po blocích. U matice A si tyto bloky označme
se tedy násobí po blocích. U matice A si tyto bloky označme 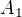 až
až  . Celá matice
. Celá matice  bude komutovat s maticí
bude komutovat s maticí  právě když budou komutovat bloky
právě když budou komutovat bloky 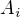 s příslušnými bloky matice
s příslušnými bloky matice  . Jestliže si hledanou funkci "dimenze prostoru komutujících matic" označíme
. Jestliže si hledanou funkci "dimenze prostoru komutujících matic" označíme  , platí pak
, platí pak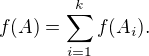
Opět se problém zjednodušil, dále můžeme předpokládat, že matice A má jediné vlastní číslo  , obecný případ pak snadno vyřešíme pomocí rovnosti na předchozím řádku.
, obecný případ pak snadno vyřešíme pomocí rovnosti na předchozím řádku.
Offline
#6 10. 11. 2012 22:18 — Editoval Pavel Brožek (10. 11. 2012 22:28)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dimenze prostoru komutujících matic
↑ check_drummer:
Ano, ukážu např. směr „pokud množina matic 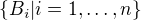 je lineárně nezávislá, pak množina matic
je lineárně nezávislá, pak množina matic 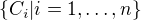 je také lineárně nezávislé“.
je také lineárně nezávislé“.
Předpokládejme, že pro nějaká 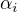 platí
platí 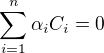 . Vynásobením rovnosti z levé strany
. Vynásobením rovnosti z levé strany  a z pravé
a z pravé 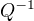 dostanu
dostanu 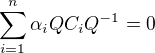 , což je
, což je 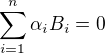 . Jenže z předpokladu nezávislosti matic
. Jenže z předpokladu nezávislosti matic  mám nulovost všech
mám nulovost všech 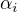 , tedy i matice
, tedy i matice 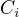 jsou nezávislé.
jsou nezávislé.
Nebo jednodušeji: zobrazení  je bijekce z prostoru matic B splňujících
je bijekce z prostoru matic B splňujících 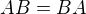 do prostoru matic C splňujících
do prostoru matic C splňujících 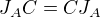 . Prostory mají tedy stejnou dimenzi.
. Prostory mají tedy stejnou dimenzi.
(Vím, že vynechávám spoustu detailů, ale kdybych se měl kompletně rozepisovat, tak by to bylo až moc dlouhé. Radši proto zodpovím doplňující otázky.)
Offline
#7 10. 11. 2012 22:42
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Dimenze prostoru komutujících matic
↑ Pavel Brožek:
Nejsem si jist, zda lze použít úvahu, že "existuje-li mezi prvky dvou vektorových prostorů bijekce, pak mají stejnou dimenzi". Např. 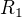 a
a 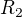 mají různé dimenze, ovšem bijekce mezi jejich prvky existuje (mají stejnou mohutnost).
mají různé dimenze, ovšem bijekce mezi jejich prvky existuje (mají stejnou mohutnost).
To ovšem nic nemění na tom, že uvedené tvrzení platí (jak jsi psal výše).
"Máte úhel beta." "No to nemám."
Offline
#8 10. 11. 2012 22:46
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Dimenze prostoru komutujících matic
↑ Pavel Brožek:
Ahoj, čekal jsem jednu z možností hodnoty dimenze: n a nebo počet vlastních vektorů, tak uvidíme...
"Máte úhel beta." "No to nemám."
Offline
#9 10. 11. 2012 22:56
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dimenze prostoru komutujících matic
↑ check_drummer:
Asi máš pravdu, měl bych být opatrnější. Tady je to lineární bijekce na konečněrozměrných prostorech, tak v takovém případě by to už snad mělo stačit.
Dimenze určitě může být větší než n, např. pro 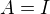 je dokonce dimenze
je dokonce dimenze  .
.
Offline
#10 10. 11. 2012 23:02
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Dimenze prostoru komutujících matic
↑ Pavel Brožek:
Ale příklad s 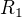 a
a 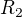 je také konečněrozměrný (nekonečný) prostor a také to nestačí...
je také konečněrozměrný (nekonečný) prostor a také to nestačí...
To je pravda - tak to asi bude naopak, dimenze by mohla být dána jako 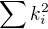 , kde
, kde  je násobnost i-tého vlastního čísla. Ale dál už radši tipovat nebudu. :-)
je násobnost i-tého vlastního čísla. Ale dál už radši tipovat nebudu. :-)
"Máte úhel beta." "No to nemám."
Offline
#11 10. 11. 2012 23:14
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dimenze prostoru komutujících matic
↑ check_drummer:
Ale neexistuje mezi nimi lineární bijekce. Ale tohle radši neřešme, ať se nebavíme o víc věcech současně, když už je to vyřešené tím druhým způsobem :-)
Nebude to tak. Záleží i na „struktuře“ podprostoru 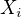 (tj. jaké tam budou Jordanovy bloky). Např. pro horní trojúhelníkovou matici 2x2 s jedničkami a jednou nulou bude dimenze 2. Pro matici 3x3 s jedním jediným vlastním číslem je dimenze prostoru komutujících matic jedno z čísel
(tj. jaké tam budou Jordanovy bloky). Např. pro horní trojúhelníkovou matici 2x2 s jedničkami a jednou nulou bude dimenze 2. Pro matici 3x3 s jedním jediným vlastním číslem je dimenze prostoru komutujících matic jedno z čísel 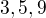 , mám tu ty případy rozepsané na papíře právě podle možného uspořádání Jordanových bloků a snažím se z toho získat nějaká obecnější tvrzení.
, mám tu ty případy rozepsané na papíře právě podle možného uspořádání Jordanových bloků a snažím se z toho získat nějaká obecnější tvrzení.
Offline
#12 11. 11. 2012 13:14 — Editoval Pavel Brožek (11. 11. 2012 13:14)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dimenze prostoru komutujících matic
Tak myslím, že mám řešení (a dokonce dokážu sestrojit všechny matice komutující s maticí  ) :-).
) :-).
Pokud  je obecná matice typu
je obecná matice typu 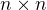 s
s  vlastními čísly
vlastními čísly  ,
, 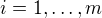 , kde každému vlastnímu číslu přísluší bloková matice složená z
, kde každému vlastnímu číslu přísluší bloková matice složená z  Jordanových bloků o velikostech
Jordanových bloků o velikostech 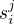 ,
, 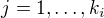 , pak dimenze prostoru komutujících matic s maticí
, pak dimenze prostoru komutujících matic s maticí  je
je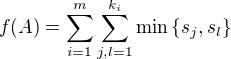
Řešení nemám sepsané úplně dopodrobna, ale tak nějak to plyne z obrázku a jeho konstrukce :-). Doplním později.
Offline
#13 11. 11. 2012 15:13 — Editoval vanok (12. 11. 2012 15:07)
Re: Dimenze prostoru komutujících matic
↑ Pavel Brožek:
Pozdr(avujem.
Najprv odkaz na wikipediu
http://fr.wikipedia.org/wiki/Paire_de_m … ommutantes
po francuzky ( ale so mnou ste si uz na to zvykol, a tak ci tak, na En nie je skoro nic)
Zakladne zname poznatky,
su Veta ktoru pises v predoslom prispevku.
Veta:
V priestore dim m, rieseni matic rovnice AX= XA ( stvorcova matica radu n)
mame equivalencie:
m=n
charakteristiky polynom A = minimalny pol. A
kazda matico co komutuje z A, je polynom matice A
veta
Dve matice (operatory), co komutuju v jednom priestore na C
maju spolocny jeden vlastny vektor
veta:
Ak naviac su diagonizable, tak maju spolocnu bazu vlastnych vektorov
veta
Majme dve matice A a B take, ze ak kazda matica matica, co komutuje z A, komutuje tiez z B, potom maatica je polynome matice A
Poznamka, aj problem "Lie bracket" v Lie algebre je tematika blizka, k tvojmu problemu.
To co som vyssie napisal je z mojich osobnych poznamok, a zda sa mi, ze je to inspirovane jednou knihou od Prasolov-a.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 12. 11. 2012 14:31 — Editoval Pavel Brožek (12. 11. 2012 21:05)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dimenze prostoru komutujících matic
K mému řešení:
Vzal jsem si matici  s jedním vlastním číslem
s jedním vlastním číslem  a hodnotami
a hodnotami 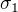 až
až  těsně nad hlavní diagonálou.
těsně nad hlavní diagonálou.  je buď nula nebo jedna (aby to odpovídalo Jordanovým blokům). Pak jsem si napsal prvek matice
je buď nula nebo jedna (aby to odpovídalo Jordanovým blokům). Pak jsem si napsal prvek matice  :
:
Rozepsal jsem si součiny  a
a 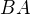 obecné matice
obecné matice  a pro komutaci dostal podmínky pro
a pro komutaci dostal podmínky pro 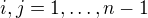 :
:
Pro ilustraci jsem si zvolil, že  bude vždy rovno jedné kromě indexů
bude vždy rovno jedné kromě indexů  a
a  , matice
, matice  tedy bude mít tři Jordanovy bloky o velikostech a, b, c. Z předchozích podmínek pak plyne, že spousta prvků matice
tedy bude mít tři Jordanovy bloky o velikostech a, b, c. Z předchozích podmínek pak plyne, že spousta prvků matice  musí být nulová a spousta prvků se „nakopíruje“ do pozice „o jeden řádek a jeden sloupec víc“ (resp. „o jeden řádek a jeden sloupec míň“). Zbylé prvky matice
musí být nulová a spousta prvků se „nakopíruje“ do pozice „o jeden řádek a jeden sloupec víc“ (resp. „o jeden řádek a jeden sloupec míň“). Zbylé prvky matice  jsou volné parametry. Na obrázku je matice B. Tmavší oranžovou jsou vybarvené prvky, které musí být 0 rovnou, světle (docházela mi fixa :-D) jsou pak nulové prvky, které se „nakopírovaly“. V nevybarvených polích (včetně „diagonál“) jsou pak volné prvky, ale tak, že v každém bloku jsou ve směru doprava dolu stejné prvky. Když si to člověk kreslí, tak je „tak nějak jasné“, že to bude vypadat stejně pro libovolný počet Jordanových bloků.
jsou volné parametry. Na obrázku je matice B. Tmavší oranžovou jsou vybarvené prvky, které musí být 0 rovnou, světle (docházela mi fixa :-D) jsou pak nulové prvky, které se „nakopírovaly“. V nevybarvených polích (včetně „diagonál“) jsou pak volné prvky, ale tak, že v každém bloku jsou ve směru doprava dolu stejné prvky. Když si to člověk kreslí, tak je „tak nějak jasné“, že to bude vypadat stejně pro libovolný počet Jordanových bloků.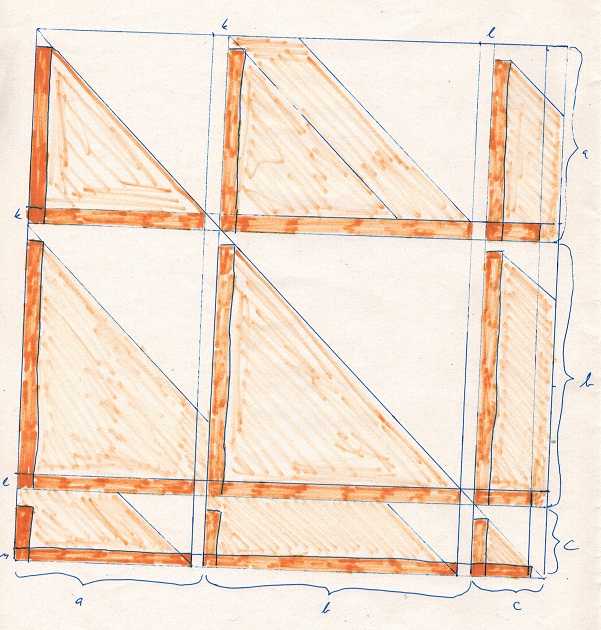
Je už snadné spočítat počet volných parametrů.
↑ vanok:
Ahoj,
díky. Jsem ale vlastně rád, že jsi svůj příspěvek napsal až po tom, co jsem si ten problém sám vyřešil. Popravdě by mě asi příliš nebavilo luštit francouzsky psaný text (pro mě je francouzština úplně cizí jazyk). Připadá mi často zábavnější vyřešit si problém sám než si prostě přečíst řešení, které je v literatuře. A ani nemám ambice tuto látku nějak více studovat nad rámec toho, co jsem si sám „vykoumal“. :-)
Sekci zajímavých úloh chápu hlavně jako možnost vyzkoušet si najít řešení pokud možno sám bez hledání jiných zdrojů na internetu.
Offline
#15 12. 11. 2012 15:06
Re: Dimenze prostoru komutujících matic
↑ Pavel Brožek:,
Ano mas pravdu, ze ide o samostatne riesenia, ale zda sa mi, ze je dobre vediet, aspon pouzivany slovnik v oblasti o ktorej pises ... tak preto som vyssie napisal, zakladne vety na tuto tematiku.
A iste tato tema ma aj aplikacie v fyzike, napr via Lie-algebry.... ale o tom nic neviem.
A co je iste, na tejto teme, pracuje vela ludi ... cize mozeme cakat pokroky....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 12. 11. 2012 20:59
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Dimenze prostoru komutujících matic
↑ Pavel Brožek:
Ahoj,
z 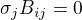 dle mého plyne, že všechny sloupce v B různé od k,l,n musí být =0. To ale v obrázku nevidím. Nebo to chápu špatně? Díky.
dle mého plyne, že všechny sloupce v B různé od k,l,n musí být =0. To ale v obrázku nevidím. Nebo to chápu špatně? Díky.
"Máte úhel beta." "No to nemám."
Offline
#17 12. 11. 2012 21:06 — Editoval Pavel Brožek (12. 11. 2012 21:07)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dimenze prostoru komutujících matic
↑ check_drummer:
Ahoj, máš pravdu, přepsal jsem se, když jsem to opisoval z papíru. Místo i tam mělo být n, opravil jsem to.
Offline