Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 11. 2012 22:40 — Editoval Honza90 (18. 11. 2012 22:46)
Re: limita posloupnosti
↑ SoniCorr:![kopírovat do textarea $\lim_{n\to+\infty }=n(\sqrt[n]{e}-1)=\lim_{n\to+\infty }n(\sqrt[n]{(1+\frac{1}{n})^{n}}-1)=\lim_{n\to+\infty }n(1+\frac{1}{n}-1)=1$](/mathtex/7e/7ed850809e29e7ddcb347edb4c043acb.gif)
Jak je ta matematika krásná :)
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#3 18. 11. 2012 22:56
Re: limita posloupnosti
↑ Honza90:
Tohle napadne skoro každého, když ten příklad uvidí, ale jak to zdůvodníš?
Offline
#6 18. 11. 2012 23:16 — Editoval Arabela (18. 11. 2012 23:22)
Re: limita posloupnosti
↑ Honza90:
lenže e sa nerovná priamo (1+1/n)^n, ale limite tohoto výrazu pre n do nekonečna...
server.gphmi.sk/~domanyov
Offline
#7 18. 11. 2012 23:18
Re: limita posloupnosti
↑ Arabela:
však n jde do nekonečna.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#8 18. 11. 2012 23:21 — Editoval Bati (18. 11. 2012 23:37)
Re: limita posloupnosti
↑ Mr.Pinker:
To já vím, o to mi nejde.
↑ Honza90:
Použil jsi tuto úpravu:![kopírovat do textarea $\lim_{n\to+\infty }n(\sqrt[n]{(1+\frac{1}{n})^{n}}-1)=\lim_{n\to+\infty }n(\sqrt[n]{e}-1)$](/mathtex/2b/2b256c59068f3dedacd974e9f142b84d.gif) (Schválně jsem to otočil)
(Schválně jsem to otočil)
Kdyby šlo takto jednoduše substituovat, jak tvrdíš, tak bych taky mohl psát třeba, že 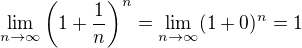 , protože
, protože 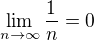 . Takže to je nesmysl a je třeba abys svou úpravu zdůvodnil.
. Takže to je nesmysl a je třeba abys svou úpravu zdůvodnil.
Offline
#11 18. 11. 2012 23:37 — Editoval Bati (18. 11. 2012 23:38)
Re: limita posloupnosti
Jo, díky, zapomněl jsem tam nko v mocnině, ale to na věci nic nemění, protože  stále platí.
stále platí.
Odpovědí na to, kde jsi udělal chybu je to, že jsi použil jisté tvrzení, které obecně neplatí, což jsem ti ukázal na tom protipříkladě. Tudíž neříkám, že tvůj výsledek je špatný, ale říkám, že nevíš, jestli je správný. To n, které jsi tam dosadil je úplně jiné n než to v původní limitě.
Offline
#13 18. 11. 2012 23:45 — Editoval Bati (18. 11. 2012 23:47)
#14 18. 11. 2012 23:48 — Editoval Honza90 (18. 11. 2012 23:55)
Re: limita posloupnosti
↑ Bati:
Upřímně, pořádně nevím proč to tak je, ale 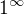 není definováno. Schválně mrkni na wolfram ;)
není definováno. Schválně mrkni na wolfram ;)
Můžeš si to zdůvodnit třeba takhle: Konvergentní posloupnost, je taková, ve které se rozdíl mezi n-tým a n+1-ním členem postupně zmenšuje, a to se tady očividně neděje.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#15 18. 11. 2012 23:54 — Editoval JohnPeca18 (19. 11. 2012 01:11)
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: limita posloupnosti
mna teda tento sposob nenapadol spis bych to delal takhle
Offline
#16 18. 11. 2012 23:56 — Editoval Bati (18. 11. 2012 23:57)
Re: limita posloupnosti
↑ Honza90:
Já vím, že 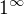 není definováno, tenhle výraz prostě nemá smysl. Ale já mám
není definováno, tenhle výraz prostě nemá smysl. Ale já mám  , což je přesně definovaný výraz.
, což je přesně definovaný výraz.
Offline
#17 18. 11. 2012 23:59
Re: limita posloupnosti
↑ SoniCorr: FJFI?
přesně to co píše ↑ Bati: píše i Pošta, když opravuje písemky, většinou k tomu příkladu ještě ale připíše 0 bodů :-D
Offline
#18 19. 11. 2012 00:02
Re: limita posloupnosti
↑ JohnPeca18:
Ano, to je asi nejrychlejší způsob. Pochopil jsem správně, že sis pod tím představil limitu funkce 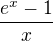 v nule a pak pomocí Heineho věty to přenesl na danou posloupnost?
v nule a pak pomocí Heineho věty to přenesl na danou posloupnost?
Offline
#20 19. 11. 2012 00:09
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: limita posloupnosti
↑ Bati:
Ano presne to som myslel.
Offline
#21 19. 11. 2012 00:13
Re: limita posloupnosti
↑ jrn:
Díky, už mě začínala přepadat zlost :) Upřímně je mi totiž líto člověka, který stvořil toto téma a místo správné rady se dozvídal věci, jako
Honza90 napsal(a):
↑ Bati:
Upřímně, pořádně nevím proč to tak je, alenení definováno. Schválně mrkni na wolfram ;)
Můžeš si to zdůvodnit třeba takhle: Konvergentní posloupnost, je taková, ve které se rozdíl mezi n-tým a n+1-ním členem postupně zmenšuje, a to se tady očividně neděje.
Offline
#24 19. 11. 2012 00:30
Re: limita posloupnosti
Nechápu, proč ti nestačí předchozí příklad spolu s tím prvním, vždy jde o stejný princip - nelze obecně počítat limitu po částech. Příklad si uděláš sám tak, že vezmeš libovolný příklad ze sbírky a dosadíš za nějaké jedno n limitní bod.
Offline
![kopírovat do textarea $\lim_{n\to+\infty }=n(\sqrt[n]{e}-1)=?$](/mathtex/43/433e67cc9f5e2173189a5dc42d2f436f.gif) údajně to má vyjít jednička. Nemám tušení jak se k tomuto výsledku dostat. Jestlis se nepletu tak cislo pod n tou odmocninou jde k jedničce. Nevíte prosím jak na to?
údajně to má vyjít jednička. Nemám tušení jak se k tomuto výsledku dostat. Jestlis se nepletu tak cislo pod n tou odmocninou jde k jedničce. Nevíte prosím jak na to?
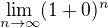 je neurčitý výraz. Nevidím na té substituci nic špatného, ani tvůj protipříklad mě zatím o ničem nepřesvědčil.
je neurčitý výraz. Nevidím na té substituci nic špatného, ani tvůj protipříklad mě zatím o ničem nepřesvědčil. nemá limitu 1?
nemá limitu 1?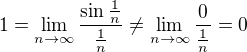
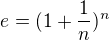 prosím
prosím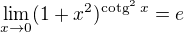 , jak se můžeš přesvědčit správným výpočtem, ale pokud bys za
, jak se můžeš přesvědčit správným výpočtem, ale pokud bys za  dosadil 0, tak ti zřejmě vyjde 1, protože jedna na jakékoliv číslo z
dosadil 0, tak ti zřejmě vyjde 1, protože jedna na jakékoliv číslo z  zůstává vždy jednou.
zůstává vždy jednou.