Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 11. 2012 17:25
- hanziczech

- Zelenáč
- Příspěvky: 21
- Škola: FEI
- Pozice: student
- Reputace: 0
Slovní úloha o pohybu
První část cyklistické trasy tvoří stoupání dlouhé 3 km, zbylou část klesání dlouhé 13 km.
Pavlova průměrná rychlost na celé trase byla dvojnásobkem jeho rychlosti na první části
trasy, jež byla o 16 km/h menší než na druhé části trasy. Za jak dlouho ujel Pavel celou
trasu?
Můj postup:
Ze zadání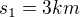
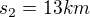
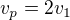
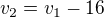
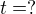
Postup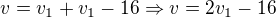
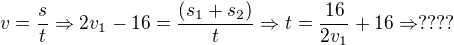
Offline
#2 28. 11. 2012 17:31
- marnes

- Příspěvky: 11227
Re: Slovní úloha o pohybu
↑ hanziczech:
1) osobně bych napsal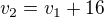
2) proč výslednou rychlost počítáš jako součet rychlostí?
Jo. A na začátku vás zdravím.
Offline
#3 29. 11. 2012 12:06 — Editoval Cheop (30. 11. 2012 14:08)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Slovní úloha o pohybu
↑ hanziczech:
První část cyklistické trasy tvoří stoupání dlouhé 3 km, zbylou část klesání dlouhé 13 km.
Pavlova průměrná rychlost na celé trase byla dvojnásobkem jeho rychlosti na první části
trasy, jež byla o 16 km/h menší než na druhé části trasy.
Za jak dlouho ujel Pavel celou trasu?
Označím:
v_1 - rychlost na prvním úseku
v_2 - rychlost na druhém úseku
t_1 - čas na prvním úseku
t_2 - čas na druhém úseku
t - celkový čas (ten máme určit)
Ze zadání lze sestavit rovnice:
1)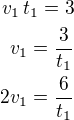 první úsek
první úsek
2)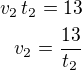 druhý úsek
druhý úsek
3)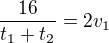 průměrná rychlost
průměrná rychlost
4)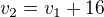 porovnání rychlostí
porovnání rychlostí
5)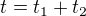 celkový čas
celkový čas
Z rovnic 2) a 4)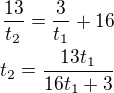 toto dosadíme do rovnice 3)
toto dosadíme do rovnice 3) 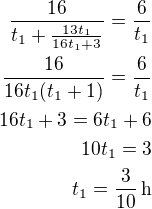
Dopočtene čas t_2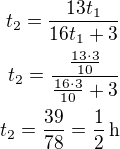
Dopočítáme celkový čas t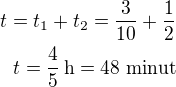
Pavel ujel celou trasu za 48 minut
Nikdo není dokonalý
Offline