Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 01. 12. 2008 17:56
Re: 2.17 Sbírka úloh 2 -Variace
↑ Lucas456:
Treba riešiť rovnicu
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 01. 12. 2008 18:40
#4 01. 12. 2008 18:43
Re: 2.17 Sbírka úloh 2 -Variace
↑ Lucas456:
Ahoj :),
nechci do toho moc lukaszh skákat, jen ti řeknu: "Rozepiš si to a uvidíš.." ;)
Offline
#5 01. 12. 2008 18:47
Offline
#8 01. 12. 2008 19:32
Re: 2.17 Sbírka úloh 2 -Variace
Ivana napsal(a):
Já sem debil :-D známý postup
Offline
#10 01. 12. 2008 21:39
Re: 2.17 Sbírka úloh 2 -Variace
Ivana napsal(a):
Proč tam škrtáš ten větší faktoriál?
Offline
#11 01. 12. 2008 21:49
Re: 2.17 Sbírka úloh 2 -Variace
↑ Lucas456:
Představ si místo toho faktoriálu jakékoliv číslo např.30 pak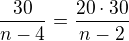
Těch 30 můžeš přece vykrátit to znamená, že můžeš vykrátit i n!
Offline
#12 01. 12. 2008 21:51
Re: 2.17 Sbírka úloh 2 -Variace
Chrpa napsal(a):
↑ Lucas456:
Představ si místo toho faktoriálu jakékoliv číslo např.30 pak
Těch 30 můžeš přece vykrátit to znamená, že můžeš vykrátit i n!
Abych se zbavil n! přidám tam další
Offline
#13 01. 12. 2008 21:54
Re: 2.17 Sbírka úloh 2 -Variace
↑ Lucas456:
Nepřidáš tam další já ti jen vysvětloval, že jak můžeš zkrátit tu 30 tak můžeš zkrátit
i ten n!
Offline
#14 01. 12. 2008 21:57
Re: 2.17 Sbírka úloh 2 -Variace
Chrpa napsal(a):
↑ Lucas456:
Nepřidáš tam další já ti jen vysvětloval, že jak můžeš zkrátit tu 30 tak můžeš zkrátit
i ten n!
No prostě to nemůžu řešit jako rovnici s faktoriály dalo by se říct.
Offline
#15 01. 12. 2008 22:03 — Editoval Chrpa (01. 12. 2008 22:05)
Re: 2.17 Sbírka úloh 2 -Variace
↑ Lucas456:
Právě, že to musíš řešit jako faktoriály.
Ale ohledně toho krácení toho n!
Teď na chvíli zapomeň na faktoriály.
Jak upravíš toto: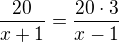
Tu 20 můžeš klidně zkrátit, protože jsou obě v čitateli zlomku
a jsou na opačné straně rovnice.
A teď si místo té 20 na obou stranách představ n! a můžeš ho
zkrátit úplně stejně jako číslo 20, protože jsou obě čísla stejná. n! = n!)
Offline
#16 02. 12. 2008 06:59
Re: 2.17 Sbírka úloh 2 -Variace
Chrpa napsal(a):
↑ Lucas456:
Právě, že to musíš řešit jako faktoriály.
Ale ohledně toho krácení toho n!
Teď na chvíli zapomeň na faktoriály.
Jak upravíš toto:
Tu 20 můžeš klidně zkrátit, protože jsou obě v čitateli zlomku
a jsou na opačné straně rovnice.
A teď si místo té 20 na obou stranách představ n! a můžeš ho
zkrátit úplně stejně jako číslo 20, protože jsou obě čísla stejná. n! = n!)
Vždy sem slyšel že se krátít do kříže tak toto je pro mě novinka.
Offline
#17 02. 12. 2008 08:20 — Editoval Cheop (02. 12. 2008 08:22)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: 2.17 Sbírka úloh 2 -Variace
↑ Lucas456:
Můžeš to zapsat i takto: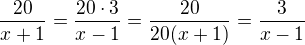 teď už vidíš, že tu 20 můžeš zkrátit.
teď už vidíš, že tu 20 můžeš zkrátit.
Nebo to můžeš zapsat i takto se stejným výsledkem: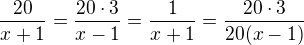
Proč by jsi to tedy převáděl na druhou stranu rovnice, když to můžeš zkrátit rovnou.
Nikdo není dokonalý
Offline
#18 02. 12. 2008 08:22
Re: 2.17 Sbírka úloh 2 -Variace
↑ Lucas456:
1. S rovnicí, kterou jsem napsala pracuješ tak, jak ti popsal ↑ Chrpa:.
2. V rovnici se objeví složený zlomek.
3. Možná by nebylo od věci zopakovat si počítání se složenými zlomky. :-)
4. Nápověda -
a/ zlomek je naznačené dělení
b/ při dělení zlomku zlomkem (složený zlomek) : první zlomek opíšeme a druhý zlomek převrátíme.. a případně zkrátíme .. tak jak je uvedeno v mém příspěvku .
Ok ?
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#20 14. 01. 2009 19:05
Re: 2.17 Sbírka úloh 2 -Variace
↑ Lucas456:Zdravím ..:-)
... tak tedy pokračuji : 
Jedna krát jedna je " tisíckrát " jedna :-)
Offline


