Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 12. 2012 15:41
Integrál
Ahoj, potřeboval bych vypočítat jeden složitý příklad. Netuším jak se to řeší tak budu rád za vaší pomoc.
Zadáno:
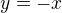
http://imageshack.us/photo/my-images/845/beznzvumk.png/
A potřebuji vypočítat plochu toho žlutého.
Děkuji
Offline
- (téma jako vyřešené označil(a) jelena)
#2 12. 12. 2012 16:02
Re: Integrál
najdi ty dva body, kde se setkávají obě fce...tedy -x=2x-x^2..což je jednoduchá kvadratická rce.
plocha ... to je určitý integrál - integrál z a do b ...v tomto případě je a to menší x z předchozí rce a b je větší x.
žlutá plocha je rozdíl dvou ploch
1 + 1 = 1
Offline
#4 12. 12. 2012 16:15
Re: Integrál
↑ hfungus:
Nemohl bys mi to prosím nějak kompletně vypočítat? Vážně to ted v té matice moc nepobírám....
Offline
#6 12. 12. 2012 16:27 — Editoval hfungus (12. 12. 2012 16:34)
Re: Integrál
3x-x^2=0 ... x(3-x)=0 ... x1=0 x2=3 toto jsem vydedukoval z obrázku...že jeden graf je nahoře, druhý dole mi říká, co mám od čeho odečíst
toto jsem vydedukoval z obrázku...že jeden graf je nahoře, druhý dole mi říká, co mám od čeho odečíst

![kopírovat do textarea $zlplocha = \frac{3}{2}[x^2] -\frac{1}{3}[x^3]$](/mathtex/a7/a71b78595cad4a32b7458920dd72674f.gif) kde x je od 0 do3
kde x je od 0 do3 ty nuly už nepíšu...kdyby onen určitý integrál nebyl od nuly ale od jiného čísla, odečítal bys ještě hodnoty předchozího vyjádření v tomto čísle
ty nuly už nepíšu...kdyby onen určitý integrál nebyl od nuly ale od jiného čísla, odečítal bys ještě hodnoty předchozího vyjádření v tomto čísle úpravy..
úpravy..
1 + 1 = 1
Offline
