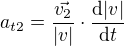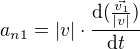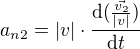Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 12. 2012 12:32
zrychlení, pohyb po elipse
Dobrý den, nevím si rady s jednou úlohou z kinematiky.
Ze zadání  ,
,  jsem zjistil, že se jedná o eliptický pohyb s rovnicí
jsem zjistil, že se jedná o eliptický pohyb s rovnicí  .
.
A teď mám zjistit složky rychlosti a zrychlení.
Ryhlosti jsou podle mě: 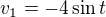
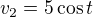
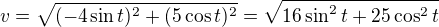
a teď zrychlení nevím, má vyjít: 

Offline
- (téma jako vyřešené označil(a) APavlat)
#2 29. 12. 2012 16:27
Re: zrychlení, pohyb po elipse
Prosím poraďte mi někdo. Zkoušel sem počítat  jako
jako 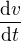 , to vyjde
, to vyjde 
z toho absolutní hodnota se rovná součtu složek  viz wolfram.
viz wolfram.
Ale pořád nevím, jak zjistit složky  a
a 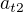 a hlavně jak na normálové zrychlení
a hlavně jak na normálové zrychlení 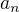 . U kružnice bych jel v pohodě přes
. U kružnice bych jel v pohodě přes  , ale jak to tady využít nevim.
, ale jak to tady využít nevim. 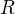 by zde mohlo být závislé na poloze, jakože
by zde mohlo být závislé na poloze, jakože  bude mířit skoro doprostřed.
bude mířit skoro doprostřed.
Offline
#3 29. 12. 2012 18:42 — Editoval FliegenderZirkus (29. 12. 2012 18:46)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: zrychlení, pohyb po elipse
Ahoj, jdeš na to správně. Hledáme vektor tečného zrychlení a známe jeho velikost
a směr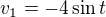 ,
, 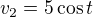 .
.
Stačí tedy vyjádřit jednotkový vektor ve směru vektoru rychlosti a ten vynásobit výše spočítanou délkou.
Normálové zrychlení se spočítá buďto použitím obecně platného vzorce, nebo jako rozdíl vektoru celkového a tečného zrychlení.
Offline