Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 12. 2012 15:15 — Editoval jarrro (29. 12. 2012 15:16)
konvergencia radu
čaute musí byť
rad 
nutne konvergentný ak je f spojitá funkcia v okolí nuly?
totiž je úloha nájsť normu takého operátora (norma na spojitých fciách je suprémum absolútnej hodnoty) nie je zložité ukázať, že je to 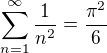 , ale
, ale
zaujíma ma či je to vôbec vždy definované (asi áno keď je to v Lukešovom Úvode do funkcionální analýzy)
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#2 29. 12. 2012 15:47
Re: konvergencia radu
↑ jarrro:
Ak f je spojitá v okolí nuly, tak je tam aj ohraničená. Teda máme konštantu M takú, že f(1/n)<M.
Z toho by nemalo byť ťažké overiť Cauchyho podmienku.
Offline

