Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 01. 2013 22:29
Derivace #8
Dobry vecer, mam zderivovat ,ale nevychazi mi to .. vysledek : http://www.wolframalpha.com/input/?i=lo … derivative
,ale nevychazi mi to .. vysledek : http://www.wolframalpha.com/input/?i=lo … derivative
Pocital jsem takhle
je to prozatim dobre nebo ne ?
Dekuji.
Offline
- (téma jako vyřešené označil(a) frantax)
#2 01. 01. 2013 22:33 — Editoval ((:-)) (01. 01. 2013 22:41)
Re: Derivace #8
↑ frantax:
Podľa mňa - derivuješ logaritmus, potom tú zátvorku za ln (a v nej aj x) a ešte aj x na druhú, ktoré je pod odmocninou...
Vždy, keď je vo "vzorci" niečo iné ako priamo x, treba ešte násobiť deriváciou toho "niečoho"...
Offline
#3 01. 01. 2013 22:34
Re: Derivace #8
Derivuj prvni soucet v logaritmu. Odmocninu mas zase slozenou fci, takze derivuj vnitrek, pak odmocninu. A pote teprve derivuj logaritmus.
Tbuj vysledek je spatne. Nevidim tam nikde derivovane x^2 ani derivovane x.
Miluju veci, kterym nerozumim!
Miluju matematiku!
Offline
#5 01. 01. 2013 23:36
Re: Derivace #8
↑ Emca21:
Diky vsem, cely priklad je takhle 
tu levou polovinu jsem zderivoval takhle : 
Ted kdyz to dam dohromady s tou pravou polovinou tak by melo vyjit podle skript
Kdyz to dam dohromady ve WA tak vyjde tohle : http://www.wolframalpha.com/input/?i=%2 … 29%29%2B2x
Divné :(
Offline
#6 01. 01. 2013 23:43 — Editoval Emca21 (01. 01. 2013 23:46)
Re: Derivace #8
↑ frantax:
ta leva strana bez toho vyrazu, ktery jsem zderivoval vys by mela vyjit takto (bez upravy)
Miluju veci, kterym nerozumim!
Miluju matematiku!
Offline
#8 01. 01. 2013 23:51
#9 01. 01. 2013 23:55 — Editoval Emca21 (01. 01. 2013 23:56)
Re: Derivace #8
↑ frantax:
Ty jo, tak to nevim jak jsi to derivoval, ale rekl bych, ze to mas blbe.  zderivujes na 2x
zderivujes na 2x zderivujes jako soucin. Tzn prvni derivujes x..vynasobis odmocninou a pak k tomu prictes derivovanou odmocninu, coz je slozena fukce a tuhle derivaci das krat x.
zderivujes jako soucin. Tzn prvni derivujes x..vynasobis odmocninou a pak k tomu prictes derivovanou odmocninu, coz je slozena fukce a tuhle derivaci das krat x.
Chapes?
Miluju veci, kterym nerozumim!
Miluju matematiku!
Offline
#11 02. 01. 2013 00:04
Re: Derivace #8
↑ frantax:
to 2x tam mam a ten zbytek jsem delal jako soucin fci, tak jak si napsal :)
Offline
#12 02. 01. 2013 00:08
Re: Derivace #8
↑ frantax:
Projed si to cele jeste jednou a porovnej muj vysledek s tvojim. Mas podle me spatne uz tu derivaci. S tim pak souvisi i spatny vysledek pri uprave.
Miluju veci, kterym nerozumim!
Miluju matematiku!
Offline
#14 02. 01. 2013 00:26
Re: Derivace #8
↑ frantax:
X^2 jsem zderivoval jako 2X , potom  tam je soucin fci. to me vyslo
tam je soucin fci. to me vyslo 
Offline
#15 02. 01. 2013 00:27 — Editoval Emca21 (02. 01. 2013 00:29)
Re: Derivace #8
↑ frantax:
Uz tam mas chybu. Zapomnel jsi u posledniho clenu zderivovat jeste vnitrni funkci pod odmocninou. Z te ti vznikne v citateli 2x.
Takhle to bude
Miluju veci, kterym nerozumim!
Miluju matematiku!
Offline
#16 02. 01. 2013 00:31 — Editoval frantax (02. 01. 2013 00:54)
Re: Derivace #8
↑ Emca21:
aha jo, to chapu , ted to zkusim dat dohromady s tim zbytkem.
Tak celkovy vysledek ted vysel takhle : http://www.wolframalpha.com/input/?i=%2 … 29%5E1%2F2
zas jinac nez ve skriptech, tam to vyslo takhle : 
Offline
#17 02. 01. 2013 00:59
Re: Derivace #8
↑ frantax:
Nevim, jak jsi upravoval. Jestli zitra (vlastne dneska) budu mit cas, tak si to prepoctu a upravim a napisu jak mi to vyslo :-) Ted uz jdu spat.. Mej se hezky :-)
Miluju veci, kterym nerozumim!
Miluju matematiku!
Offline
#19 02. 01. 2013 01:41 — Editoval Jan Jícha (02. 01. 2013 01:49)
- Jan Jícha

- Veterán

- Místo: Plzeň/Mnichov
- Příspěvky: 1801
- Škola: ZČU - FST - KMM
- Pozice: Safety Engineer
- Reputace: 74
- Web
Re: Derivace #8
Ahoj, většinou bych se na to vykašlal a šel spát, ale protože teď v lednu dělám taky zkoušku z matiky (a jsou tam i derivace), tak si to procvičím. :-))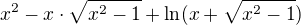
Derivace



Nechce se mi to upravovat ani rozšiřovat teď v noci, ale jsem si jist, že je to dobře a pokud to správně upravíš, dostaneš požadovaný tvar 
J.J.
Edit: To jsem celej já, místo toho abych se učil na zkoušku z Managementu, kterou mám v pátek, a docela to ještě neumím, tak tu vysedávám do noci a sepisuju slohy v LaTeXu :-D
Offline
#20 02. 01. 2013 20:06
Re: Derivace #8
↑ Jan Jícha:
Ok diky moc, za ty derivace, ale stejne nevim jak se dostanu k tomu tvaru ve skriptech ...:(
Offline





