Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » uspořádání, vnoření, příklad (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 01. 2013 11:57
uspořádání, vnoření, příklad
Dobrý den.
Přemýšlím nad příkladem z knihy Kapitoly z diskrétní matematiky od vážených autorů Matoušek, Nešetřil.
Dokaž, že existuje konečná částečně uspořádaná množina, jíž nelze vnořit do  , kde
, kde
Nemohu přijít na řešení. Ani v analogickém dvoudimenzionálním případě  .
.
Nakonec mi zůstal jediný nápad. Protože každou uspořádanou množinu  lze vnořit do
lze vnořit do  , a protože složení vnoření je vnoření, musí existovat
, a protože složení vnoření je vnoření, musí existovat 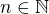 a
a  , že
, že  nelze vnořit do usp. mn. ze zadání. To se mi zdá ale složité.
nelze vnořit do usp. mn. ze zadání. To se mi zdá ale složité.
( )
)
Díky za rady.
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 06. 01. 2013 14:24 — Editoval anes (06. 01. 2013 14:26)
Re: uspořádání, vnoření, příklad
Ahoj, myslím, že pro R2 bych něco viděl. Rozmysli si, jak vypadá nějakých n prvků, které jsou při tom uspořádání  vzájemně nesrovnatelné. To bude množina
vzájemně nesrovnatelné. To bude množina  taková, že
taková, že  buď
buď  , nebo
, nebo  . To je ale dost velké omezení, které ovlivní, jak si tato n-tice prvků může stát ve srovnání s ostatními.
. To je ale dost velké omezení, které ovlivní, jak si tato n-tice prvků může stát ve srovnání s ostatními.
Dokončení (spoiler)
Pro R3 jsem si protipříklad konstruovat nezkoušel, tam to bude trochu pracnější, ale jsem si celkem jistý, že analogická úvaha půjde použít i tam. Ale to mé řešení je jen takové vyrobené na koleně, tak tě třeba hned napadne nějaká obecnější formulace toho, co jsem tu popsal.
Offline
#3 06. 01. 2013 14:38
Re: uspořádání, vnoření, příklad
↑ anes:
Děkuji za odpověď. Můj první nápad byl, že asi neexistuje nekonečný antiřetězec, ale pak jsem jej sestrojila :D
Promyslím si Tvou radu.
What does a drowning number theorist say?
'log log log log ...'
Offline
#8 06. 01. 2013 15:28
Re: uspořádání, vnoření, příklad
↑ pf:
Super, tak to je hezké.
Kdybyste chtěli pokračovat zajímavostmi, pište dál :)
Já děkuji a teď si to pomalu zpracuji.
What does a drowning number theorist say?
'log log log log ...'
Offline
#9 06. 01. 2013 16:49
Re: uspořádání, vnoření, příklad
↑ Andrejka3:
Jo. Tak, jak jsem to já napsal, by bylo ještě prohozené  ,
,  , což je úplně fuk. A za promyšlení to ještě možná stojí. Kromě toho, že se tu udělá dost snadno chyba (což snad v tom mém předchozím příspěvku není, ale...), já jsem vycházel z toho, že množina nesrovnatelných prvků má nějaký speciální tvar (který by se mohl pro vyšší dimenze komplikovat).
, což je úplně fuk. A za promyšlení to ještě možná stojí. Kromě toho, že se tu udělá dost snadno chyba (což snad v tom mém předchozím příspěvku není, ale...), já jsem vycházel z toho, že množina nesrovnatelných prvků má nějaký speciální tvar (který by se mohl pro vyšší dimenze komplikovat).
Přitom by asi bylo výhodnější řešit to (aspoň teď, když už tušíme, jak na to) "odshora". Mohli jsme začít naložením podmínek
,
,
,
,
,
nesrovnatelné,
(ze kterých pochopitelně ta nesrovnatelnost a,b,c vyplývá), a pouhým rozepisováním vztahů v jednotlivých složkách dojít ke sporu. To bude asi mnohem lepší postup pro zobecňování...
Jednoduchý návod pro výrobu protipříkladů k vnořitelnosti do  .
.
A teď proč to sem píšu, když už to řešení asi nějak z předchozí debaty v podstatě vyplynulo:
1) Vidí někdo na první pohled, jestli šel ten tvar problematických množin nějak "uspokojivě" odvodit? Tím zkoumáním v duchu mého prvního příspěvku bych se asi řešení našlo, ale dost pracně. Přitom v této úloze je určitě hromada symetrií, tak by možná nějaký dobrý nápad pomohl.
2) Ta otázka vnořování potenční množiny, k tomu existuje nějaká teorie, která nám s naší úlohou může pomoct, nebo se to tu objevilo jen jako zajímavý důsledek? Tak trochu jsem totiž čekal, že po vykreslení grafu
 bude ta problematická množina odpovídat nějakým dvěma sousedním patrům z prostředka. Přitom je mnohem menší, odpovídá patrům 1 a n-1. Znamená to něco, neumí se to nějak přeformulovat, že by se třeba ukázalo, že je ta úloha ekvivalentní něčemu jinému? Nešel by z toho třeba vytřískat nějaký vyčerpávající popis problematických množin?
bude ta problematická množina odpovídat nějakým dvěma sousedním patrům z prostředka. Přitom je mnohem menší, odpovídá patrům 1 a n-1. Znamená to něco, neumí se to nějak přeformulovat, že by se třeba ukázalo, že je ta úloha ekvivalentní něčemu jinému? Nešel by z toho třeba vytřískat nějaký vyčerpávající popis problematických množin? Offline
#10 06. 01. 2013 17:16 — Editoval Andrejka3 (06. 01. 2013 18:00)
Re: uspořádání, vnoření, příklad
↑ anes:
1) V tomto příkladu mé první pohledy selhaly. Očekávám, že nějakou intuici si vytvořím, jakmile to řešení uspokojivě zapíšu do svých osobních `skript'. Zatím jsem u Tvé myšlenky R2, pak chci nějak posoupit k tem  .
.
Hromad symetrií se děsím, protože se bojím, že to neuvidím.
2)  nešlo vnořit do
nešlo vnořit do  ,
,
kolega pf tvrdil, že nelze vnořit do
nelze vnořit do  , odkud mě napadlo to tvrzení pro libovolné
, odkud mě napadlo to tvrzení pro libovolné  .
.
Zatím nevím, jak obecně dokázat, ani jak dokázat v případě R3. Protože jste mi ale poskytli návody, řekla jsem si, že to zkusím dokončit :)
Taky jsem si myslela, že problémové usp.mn. jsou prostřední patra  (ta nejširší).
(ta nejširší).
Nevím, co jde vytřískat, zatím jsi rychlejší než já :) Samozřejmě mě to ale zajímá.
Edit: Snad jsem odpověděla na otázku..
What does a drowning number theorist say?
'log log log log ...'
Offline
#11 06. 01. 2013 19:42 — Editoval Andrejka3 (06. 01. 2013 19:43)
Re: uspořádání, vnoření, příklad
↑ anes:
Jednoduchý návod pro výrobu pro výrobu problematických množin je hezký. Jak píšeš, odpovídá patrům  druhému odshora a odpoda. Až teď mi to vše zapadlo do sebe.
druhému odshora a odpoda. Až teď mi to vše zapadlo do sebe.
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » uspořádání, vnoření, příklad (TOTO TÉMA JE VYŘEŠENÉ)

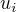 (
( sestupně dle
sestupně dle  ). Pokud pro nějaké
). Pokud pro nějaké 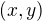 platí
platí  a
a  , pak z definice
, pak z definice  také pro všechny indexy
také pro všechny indexy  mezi
mezi  .
. , kde
, kde  budou vzájemně nesrovnatelné (naše n-tice),
budou vzájemně nesrovnatelné (naše n-tice),  je vedle
je vedle  ,
,  a zároveň
a zároveň  (tj.
(tj.  nelze vnorit
nelze vnorit  ...
... .
. prvcích,
prvcích,  ,
,  tak, že
tak, že  pro
pro  a
a  s
s 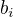 nesrovnatelné.
nesrovnatelné. je některá ze složek vektoru
je některá ze složek vektoru  (a my jsme přitom na \mathbb{R}^n).
(a my jsme přitom na \mathbb{R}^n).