Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Inetgrace parciálních zlomů, prosím o kontrolu.
#1 12. 01. 2013 16:06 — Editoval Bodye (12. 01. 2013 16:08)
Inetgrace parciálních zlomů, prosím o kontrolu.
Zdravím, chtel bych nekoho poprosit, jestli by mi neprojel reseni tohodle prikladu, dekuji.
A ted z toho vyleze:
Dále:

po dosazeni:

kde


kde 
po dosazeni
prvni integral
a druhy
substutice a vyjde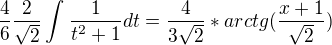
Potom kdyz to dame dohromady:
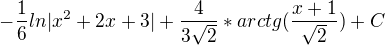
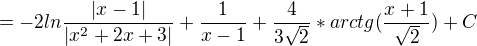
tady si nejsem jist s tou upravou toho logaritmu, to bude asi spatne.
Offline
#2 12. 01. 2013 17:00 — Editoval marnes (12. 01. 2013 17:02)
- marnes

- Příspěvky: 11227
Re: Inetgrace parciálních zlomů, prosím o kontrolu.
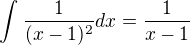 tímto si nejsem jist dle mého
tímto si nejsem jist dle mého 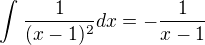
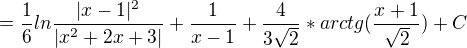 a když tak se ten zlomek dá napsat do jedné AH
a když tak se ten zlomek dá napsat do jedné AH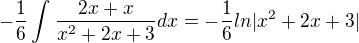 tady v čitateli místo x má být 2, ale jinak integrál ok
tady v čitateli místo x má být 2, ale jinak integrál ok
to je co bych okomentoval já
Jo. A na začátku vás zdravím.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Inetgrace parciálních zlomů, prosím o kontrolu.