Matematické Fórum

Marian · 05. 12. 2008 02:31 — Editoval Marian (06. 12. 2008 20:52)

Zrovna jsem řešil relativně zajímavou limitu posloupnosti. Ať se neztratí tato úloha mezi úlohami o teorii grafů a kombinatorice ve fóru pro VŠ, píši úlohu sem. Tedy ...

Vypočtěte limitu posloupnosti
$\Large\lim_{n\to\infty}\nosmash\quad\left ((n+1)!^{\frac{1}{n+1}}-n!^{\frac{1}{n}}\right ).$

Ve spojitosti s touto úlohou si vzpomínám ještě na jednu limitu z Děmidovičovy sbírky, která by se snad mohla řešit podobně (teď už to zkoušet nebudu ;) a tuším, že při jejím řešení jsme se s Pavlem zasekli. Jedná se o úlohu 1370, kde se má spočítat limita funkce
$\Large\lim_{x\to\infty}\nosmash\quad\left ((x+a)^{1+\frac{1}{x}}-x^{1+\frac{1}{x+a}}\right ).$

Marian · 05. 12. 2008 13:52

↑ Pavel:

Vážím si tvého velkého snažení, ale musím přiznat, že když jsem to psal, tak jsem v zadání zapomněl jistou vánoční ozdobu, totiž faktoriál. Úlohu, kterou jsem chtěl zadat má vypadat takto: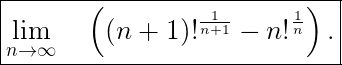
$\boxed{\Large\lim_{n\to\infty}\nosmash\quad\left ((n+1)!^{\frac{1}{n+1}}-n!^{\frac{1}{n}}\right ).}$

A co se týče limity, kterou počítáš ty, dá se to spočítat z hlavy, neboť
$\lim_{n\to\infty}\nosmash\quad\left ((n+1)^{\frac{1}{n+1}}-n^{\frac{1}{n}}\right ) =\lim_{n\to\infty}\sqrt[n+1]{n+1}-\lim_{n\to\infty}\sqrt[n]{n}=1-1=0.$

Ale ta poopravená limita je podstatně zajímavější. Takže omlouvám se, že jsem zájemce zatížil bezvýznamnou úlohou - ale náprava je uvedena v tomto příspěvku.

Marian · 06. 12. 2008 14:07 — Editoval Marian (06. 12. 2008 16:06)

Zatím je nějaký velký klid při řešení této úlohy. Tedy malá nápověda z mé strany je ta, že mě napadlo použít jistým způsobem a aplikovat identitu
$\lim_{x\to 0}\frac{e^x-1}{x}=1.$

halogan · 06. 12. 2008 18:06

↑ Marian:

Prosímvás, Mariane, nechcete danou nápravou provést i v úvodním příspěvku? Věřím, že řešitel si nebude chtít pročítat odpovědi ostatních před řešením a při kontrole pak asi nechce zjistit, že počítal něco jiného.

Marian · 06. 12. 2008 20:53

↑ halogan:

Opraveno! A, prosím tě, nevykej mi ...
:-)

math.oaf · 06. 12. 2008 23:29

len taký pokus o riešenie tej limity z Děmidoviča 1370:
$\lim_{x\to\infty}\nosmash\quad\left ((x+a)^{1+\frac{1}{x}}-x^{1+\frac{1}{x+a}}\right )=\lim\limits_{ x \to \infty}[x(x+a)^{\frac{1}{x}} +a(x+a)^{\frac{1}{x}} -xx^{\frac{1}{x+a}}]=$
${\lim}\limits_{ x \to \infty}x*{\lim}\limits_{x \to \infty}(x+a)^{\frac{1}{x}}+{\lim}\limits_{x \to \infty}a*{\lim}\limits_{x \to \infty}(x+a)^{\frac{1}{x}}-{\lim}\limits_{x \to \infty}x*{\lim}\limits_{x \to \infty}x^{\frac{1}{x+a}}=$ , kedze a=konst a ${\lim}\limits_{x \to \infty}\sqrt[x]{x}=1$ dostavame:
$={\lim}\limits_{x \to \infty}x*1+{\lim}\limits_{x \to \infty}a*1-{\lim}\limits_{x \to \infty}x*1={\lim}\limits_{x \to \infty}a=a$ , snad je postup dobre :D.

Pavel Brožek

↑ math.oaf:

Postup není dobře, odečítáš od sebe dvě nekonečna.

↑ Marian:

K první limitě - napadlo mě spočítat 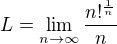$L=\lim_{n\to\infty}\frac{n!^{\frac1n}}{n}$ a pak ukázat (zavedu funkci 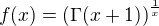$f(x)=$\Gamma(x+1)$^{\frac1x}$ ), že zde platí 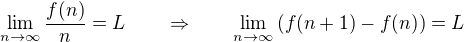$\lim_{n\to\infty}{\frac{f(n)}n}=L\qquad\Rightarrow\qquad\lim_{n\to\infty}{(f(n+1)-f(n))=L}$ . Dál jsem se zatím nedostal, nemám teď bohužel moc času.

Marian · 08. 12. 2008 10:07 — Editoval Marian (08. 12. 2008 13:13)

↑ BrozekP:

Nepopírám, že to takto půjde, jistě by se musely rozebrat některé drobnosti. Myslím, že toto fórum není jen o jediném řešení; jsem velice rád, že přístupů je několik. Své řešení si nechám pro sebe zatím, počkám(e) na ostatní, s čím přijdou.

↑ math.oaf:
Výseledek má vyjít $a$ , ale s postupem také nesouhlasím. Zatím jsem neměl čas se na tu limitu kouknout lépe - provedu co nejrychleji.
Editace. Tak už jsem spočetl limitu funkce v mém původním příspěvku. Čekám tedy již jen na nápady ostatních.

Jen ještě drobná poznámka - limita $\lim_{n\to\infty}\frac{\sqrt[n]{n!}}{n}$ je známa. Nezajímá mě ale, co se najde v tabulkách, pokud kdosi tuto limitu použije, chci i důkaz toho, že tato limita se rovná ... (doplňte sami). A protože se jedná o limitu posloupnosti, rád bych (mimo jiné - třeba BrozekP-ova poznámka o funkci GAMMA) postupy, které se používají před zavedením diferenciálního počtu. Možná, že tuto limitu stejně "brzy" počítá v knize Diferenciání počet I i V. Jarník - nevím, nekontroloval jsem to. Bude dle mého stačit vhodně použít indukci, nebo jiná kouzla.

Marian · 08. 12. 2008 22:09 — Editoval Marian (08. 12. 2008 22:44)

Dovolil bych si tedy vyřešit limitu 1370 z Děmidovičovy sbírky. Zde je výpočet ...

Edit: Drobnosti ve výpočtu přenechávám zájemcům.

math.oaf · 09. 12. 2008 14:59

↑ Marian:
heský!

Marian · 09. 12. 2008 15:28 — Editoval Marian (09. 12. 2008 15:31)

↑ math.oaf:
Snad to ostatní (i tebe - pokud mohu tykat) navnadí na řešení původní limity. Slevuji z požadavků.

Vypočtěte původní limitu jakkoliv chcete (myslím tu s faktoriály). Ostatní drobnosti uděláme společně. Postup je hodně podobný, více snad nemohu ani poradit, protože by to už nepatřilo do kategorie zajímavých úloh.

math.oaf · 10. 12. 2008 20:11

↑ Marian:
joj ked budem mat cas tak aj tu skusim, no som zvedavy... :D

math.oaf · 14. 12. 2008 22:07

↑ Marian:
Tak už som to pozrel, a dufam, že to je dobre :D (mimochodom, jasne že mi môžeš tykať, nie som ani dost starý ani inteligentný, aby mi ktosi vykal :D), použil som toho tvojho návodu, dúfam, že si to myslel tak nejako..., aj nápad kolegu zhora pouzit $\lim_{n\to\infty}\frac{\sqrt[n]{n!}}{n}$ :

no a este pouzitim jednej veticky som ju určil takto:

Marian · 15. 12. 2008 23:27

↑ math.oaf:

Výborně! Do Vánoc určitě něco zajímavého přibude ...
:-)

math.oaf · 16. 12. 2008 09:05

↑ Marian:
Dik, ale bez toho návodu, no neviem kam by som sa dostal :D

zeta · 01. 11. 2009 15:18

Prosím Vás , potřebuji vypočítat limita posloupnosti , ale bohužel jsem nepochopila ani to , jak se píše na klávesnici třeba odmocnina apod. tak to píšu slovy, snad to pochopíte.

lim ( odmocnina 2n + 1 - odmocnicna n ) =

výsledek je nekonečno, ale ráda bych věděla, jak se k tomu dospělo.

Další příklad.

lim (odmocnina 2n + 1 - odmocnina 2n

Zatím děkuji

halogan · 01. 11. 2009 15:38

↑ zeta:

Hezké nedělní odpoledne přeji.

1) Mohla byste si založit vlastní téma v sekci střední škola nebo vysoká škola? Děkuji.

2) Pozor na závorky. "odmocnina 2n + 1" by znamenalo něco jiného, než co myslíte. Chcete 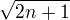$\sqrt{2n + 1}$ ? Potom prosím pište "odmocnina (2n + 1)", ať v tom máme pořádek. Děkuji.

Matematické Fórum

#1 05. 12. 2008 02:31 — Editoval Marian (06. 12. 2008 20:52)

Prosincová limita

#2 05. 12. 2008 13:52

Re: Prosincová limita

#3 06. 12. 2008 14:07 — Editoval Marian (06. 12. 2008 16:06)

Re: Prosincová limita

#4 06. 12. 2008 18:06

Re: Prosincová limita

#5 06. 12. 2008 20:53

Re: Prosincová limita

#6 06. 12. 2008 23:29

Re: Prosincová limita

#7 06. 12. 2008 23:52 — Editoval BrozekP (06. 12. 2008 23:54)

Re: Prosincová limita

#8 08. 12. 2008 10:07 — Editoval Marian (08. 12. 2008 13:13)

Re: Prosincová limita

#9 08. 12. 2008 22:09 — Editoval Marian (08. 12. 2008 22:44)

Re: Prosincová limita

#10 09. 12. 2008 14:59

Re: Prosincová limita

#11 09. 12. 2008 15:28 — Editoval Marian (09. 12. 2008 15:31)

Re: Prosincová limita

#12 10. 12. 2008 20:11

Re: Prosincová limita

#13 14. 12. 2008 22:07

Re: Prosincová limita

#14 15. 12. 2008 23:27

Re: Prosincová limita

#15 16. 12. 2008 09:05

Re: Prosincová limita

#16 01. 11. 2009 15:18

Re: Prosincová limita

#17 01. 11. 2009 15:38

Re: Prosincová limita

Zápatí