Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Separabilní metrický prostor (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 01. 2013 19:49
Separabilní metrický prostor
Ahoj všem,
učím se na analýzu a zasekl jsem se v půlce jednoho důkazu. Předem děkuji za jakoukoliv radu.
Věta: Každá část separabilního metrického prostoru je separabilní.
Můj důkaz: Označím  separabilní metrický prostor a jeho podprostor
separabilní metrický prostor a jeho podprostor  . Protože
. Protože  je sep., existuje spočetná množina
je sep., existuje spočetná množina  taková, že
taková, že  (je hustá v X).
(je hustá v X).
Nyní uvažuji systém okolí bodů z  :
:  , kde
, kde  . Označím
. Označím  jeden libovolný bod z
jeden libovolný bod z  , pokud takový existuje. Označím ještě
, pokud takový existuje. Označím ještě  . Zřejmě
. Zřejmě  a je spočetná. Budu chtít nyní dokázat, že
a je spočetná. Budu chtít nyní dokázat, že  je hustá v
je hustá v  .
.
1) Předpokládám, že  . Protože
. Protože  je hustá v
je hustá v  , existuje bod
, existuje bod  takový, že
takový, že  . Takže
. Takže  .
. 
2) Potřebuju dokázat, že  , na což právě nemohu přijít. Myslím si, že něco triviálního přehlížím, nebo mám někde chybu spíš, než že by to bylo těžké.
, na což právě nemohu přijít. Myslím si, že něco triviálního přehlížím, nebo mám někde chybu spíš, než že by to bylo těžké.
Offline
- (téma jako vyřešené označil(a) Bati)
#2 19. 01. 2013 20:18
Re: Separabilní metrický prostor
Nemel byt se ten uzaver  delat pouze v prostoru
delat pouze v prostoru  ? Potom je inkluze
? Potom je inkluze  jasna. Jelikoz chces dokazat, ze prostor
jasna. Jelikoz chces dokazat, ze prostor  je separabilni.
je separabilni.
Samozrejme pokud udelas uzaver  v
v  tak to inkluzi nedostanes napr. vem si jako
tak to inkluzi nedostanes napr. vem si jako  libovolnou hustou podmnozinu
libovolnou hustou podmnozinu  , treba iracionalni cisla, ta ma hustou spocetnou podmnozinu
, treba iracionalni cisla, ta ma hustou spocetnou podmnozinu  ale jeji uzaver musi byt cele
ale jeji uzaver musi byt cele 
Offline
#3 19. 01. 2013 20:22
Re: Separabilní metrický prostor
↑ lecopivo:
Jo, ten uzávěr je samozřejmě myšlen v  , ne v celém
, ne v celém  . Ale stejně nevidím, proč je inkluze
. Ale stejně nevidím, proč je inkluze  jasná. Vím přece jen, že
jasná. Vím přece jen, že  .
.
Offline
#7 19. 01. 2013 21:04
Re: Separabilní metrický prostor
Jasně, ten uzávěr nemůže být větší než M, neboť je to uzávěr v M. Je to tak jednoduché a přitom se mi to zdálo tak nemožné - právě kvůli tomu protipříkladu s tou otevřenou množinou, který se mi v hlavě nějak utvořil...takového promrhaného času...
Děkuji.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Separabilní metrický prostor (TOTO TÉMA JE VYŘEŠENÉ)

 je lib podmnozina
je lib podmnozina 
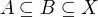 . Potom
. Potom  .
.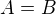 nějakou otevřenou množinu.
nějakou otevřenou množinu.


 je uzaver
je uzaver  je uzaver
je uzaver