Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Cramerovo pravidlo (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 12. 2008 11:27
- Klara-Novotna

- Příspěvky: 33
- Reputace: 0
Cramerovo pravidlo
Uzitim Cramerova pravidla vyreste následující stoustavu rovnic
Prosím Vás potřebovala bych, kdyby mi s tímto příkladem někdo pomohl. Děkuji
Offline
#2 14. 12. 2008 11:30
Re: Cramerovo pravidlo
↑ Klara-Novotna:
Neviem v čom presne máš problém, pri Cramerovom pravidle je postup priamočiary. Len vypočítaš príslušné determinanty.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 14. 12. 2008 11:57
- Klara-Novotna

- Příspěvky: 33
- Reputace: 0
Re: Cramerovo pravidlo
Vypocitala jsem determinanty pomoci excelu. Nejsem si presne jista jak se dela determinant z matice 4x4.. nizsí umim.. Kazdopadne vysledek mi vysel tatko:
x1 = 1
x2=0
x3=0
x4=-1
Nemohl by to prosim nekdo overit zda-li je to spravne?
Dale kdyby se nasla nejaka dobra duse a napsala mi jak se dela determinant 4x4 byla bych velice vdecna dotycne osobe.
Děkuji
Offline
#4 14. 12. 2008 12:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Cramerovo pravidlo
↑ Klara-Novotna:
Zdravím :-)
pro kontrolu můžeš používat online kalkulátory, já používám tento: http://wims.unice.fr/wims/wims.cgi?sess … category=T (zvol matrix nebo linear solver, co potrebujes)
OK?
Offline
#5 14. 12. 2008 12:27
Re: Cramerovo pravidlo
↑ Klara-Novotna:
Ak vieš robiť Laplaceov rozvoj determinantu, tak to je prvá možnosť. Ten rozvoj sa robí nasledovne, pre 4x4 maticu: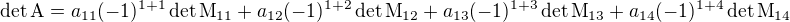
kde M_{ij} je matica, ktorá vznikne vynechaním i-teho riadka a j-teho stĺpca matice A, ktorej determinant počítaš. Keďže matice M_{ij} sú 3x3 a tých determinant vieš vypočítať, tak môžeš vypočítať det A.
Iná metóda je úpravou na horný trojuholníkový tvar, výlučne použitím úprav: pripočítanie násobku nejakého riadku k druhému. Ak použiješ iné úpravy: násobenie konštantou, výmena riadku, tak sa môže stať, že ti vyjde zlý výsledok. Ak maticu upravíš na daný tvar, potom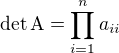
teda determinant je súčin prvkov na diagonále (pivotov).
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Cramerovo pravidlo (TOTO TÉMA JE VYŘEŠENÉ)
