Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 04. 02. 2013 21:20 — Editoval ((:-)) (04. 02. 2013 21:21)
Re: definiční obor
↑ Elisa:
Pod odmocninou musí byť číslo väčšie ako nula alebo rovné 0.
To znamená, že nezáporný musí byť zlomok.
Keďže jeho menovateľ je kladný, musí byť nezáporný jeho čitateľ.
Riešiš nerovnicu čitateľ je väčší nanajvýš rovný 0.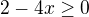
Offline
#6 04. 02. 2013 21:30
Re: definiční obor
:D f:y = to je funkční předpis, který každému prvku x z Df přiřadí právě jedno y z Hf. To je funkce. Můžeš určit sudost, lichost, kde je rostouci, klesajici, udělat jeji derivaci, kde má maxima, minima, načrtnou graf. ;) prostě funkce
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline

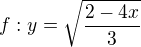

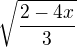 . Osobne davam prednost zapisu
. Osobne davam prednost zapisu