Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 01. 2013 12:59
prvočísla.
zase zdravím vśechny matematiky. je víkend, jsem nemocný, z toho je asi každému jasné, že se nudím. Jako vždy sem si tedy začal formulovat určité tvrzení, a jako vždy začínám pochybovat o mých schopnostech s ním něco udělat, a když už něco udělám, tak o správnosti těchto kroků.
abych byl úplně přesný, pak to, co zkusím rozebrat (a v čem by mi mohl někdo matematicky zdatnější pomoct...) mě napadlo, když sem se po delší době vrátil k mým náčrtkům Ulamova čtverce, který mě kdysi silně zaujal. Teď, jak sem se po delší době k těmto náčrtkům vrátil, a podíval se na nějaké poznámky, mám něco takového:
sloupec 1: hodnoty n
sloupec 2: hodnoty n^2 + n + 1
sloupec 3: hodnoty n^2 + n - 1
pozn. nejde mi používat tabulátor pro odsazení, má to tak být nebo je to můj problém? sem zvyklý odsazovat když se snažím programovat.
pozn. 2 : znak × nepoužívám k násobení
všimněte si, jak často jsou tyto dvojice zároveň prvočíselnými dvojcemi... Zároveň můžeme vypozorovat nějaké vztahy, jako třeba:
"Číslo
 je složené tehdy (ne pouze tehdy), existují-li
je složené tehdy (ne pouze tehdy), existují-li 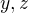 - přirozená - taková, že
- přirozená - taková, že  . to je vcelku logické, a ani bych to nemusel rozebírat, zajímavá je ale jiná věc:
. to je vcelku logické, a ani bych to nemusel rozebírat, zajímavá je ale jiná věc:budu řešit případ pro
 myslím si že pro
myslím si že pro 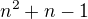 by byl postup analogický
by byl postup analogickýtakže napadlo mě, že si tyto možnosti rozepíšu - jednou pro
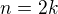 a jednou pro
a jednou pro  :
:jednou to bude
 - to když n = 2k
- to když n = 2ka po druhé
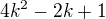 - to pro n = 2k-1
- to pro n = 2k-1vypíšeme si prvních několik členů pro různá k:
1: 3 a 7
2: 13 a 21
3: 31 a 43
.
.
.
takto to pokračuje dál... podívejte se na předchozí tabulku a na tuto a bude jasná jedna věc:
nové tvrzení: "číslo
 je složené tehdy (právě? .... to nevím) jestliže existují x,y - přirozená - taková, že
je složené tehdy (právě? .... to nevím) jestliže existují x,y - přirozená - taková, že 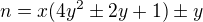
pozn.: znak
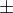 v tomto případě vyjadřuje, že na libovolný výskyt tohoto znaku může být libovolný ze znaků + nebo -.
v tomto případě vyjadřuje, že na libovolný výskyt tohoto znaku může být libovolný ze znaků + nebo -.Závěr: Asi bych potřeboval pomoct jestli mám vůbec tu poslední podmínku dobře, za druhé jestli opravdu popisuje všechny případy, kdy
 je složené a kdy ne... jestli by to náhdodou byla pravda - bylo by možné nějak matematicky popsat všechna čísla n, pro která je
je složené a kdy ne... jestli by to náhdodou byla pravda - bylo by možné nějak matematicky popsat všechna čísla n, pro která je  prvočíslo? za každou z těchto odpovědí bych byl moc vděčný. zatím příjemný den všem...
prvočíslo? za každou z těchto odpovědí bych byl moc vděčný. zatím příjemný den všem... Offline
#2 10. 02. 2013 01:03
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: prvočísla.
Protipříklad: x=1, y=1.
* oba znaky +- nahradíme +. Pak n=8, n^2+n+1=73, prvočíslo
* první +, druhý -: n=6, n^2+n+1=43, prvočíslo
* oba znaky -: n=2, n^2+n+1=7, prvočíslo.
Pro zbylou kombinaci +- je pak protipříklad x=1, y=2.
Hypotéza o složenosti by fungovala pro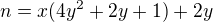

což je stejně zřejmé jako ve verzi s  .
.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#3 10. 02. 2013 10:52
Re: prvočísla.
Ano, asi je to špatně, každý může udělat chybu, a já jsem rád že můžu aspoň zkoušet něco nového. díky za upozornění. ani nevím kde sem si k tomuto příkladu věci psal, ale proškrtám si to. ale to, že to takto neplatí mě docela dost překvapilo, určitě jsem někde udělal nějakou zásadní chybu, jak je mým zvykem.
takže ještě jednou díky za upozornění, tyto příklady stejně řeším když se nudím, tak teď mám nějaký čas apoň znovu co dělat
Offline