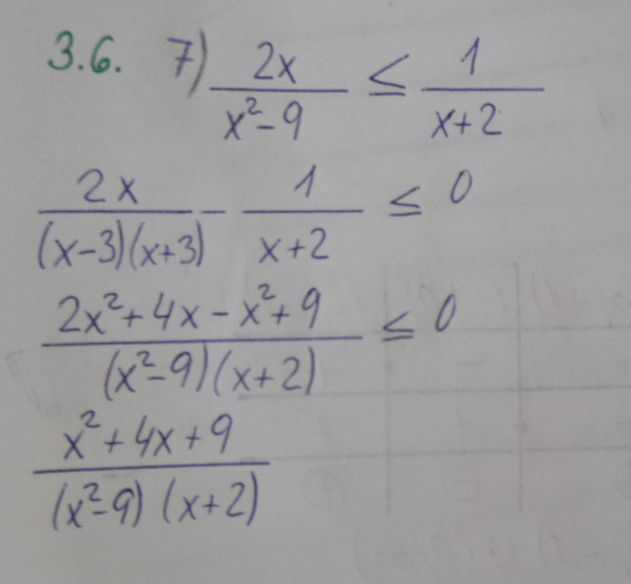Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » racionální nerovnice s jednou neznámou (TOTO TÉMA JE VYŘEŠENÉ)
#2 02. 03. 2013 16:36
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: racionální nerovnice s jednou neznámou
↑ Elisa:
Zdravím,
máte to dobře. Teď je potřeba vše co lze rozložit na součin a najít nulové body všech výrazů. Z nich pak sestavíte tabulku s intervaly a budete zkoumat znaménka.
Offline
#3 02. 03. 2013 16:47
Re: racionální nerovnice s jednou neznámou
Není třeeba nic rozkládat na součin.
Stačí jen vědět že čitatel bude vždy kladný takže se ti řešení zredukuje na rovnici:
Jelikož je čitatel kladný, tak musí být jmenovatel záporný, aby byl zlomek záporný
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 02. 03. 2013 16:55 — Editoval Freedy (02. 03. 2013 16:56)
Re: racionální nerovnice s jednou neznámou
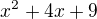
Tento čitatel jsem měl na mysli. A ten bude vždy kladný protože je diskriminant záporný a když dosadím jakoukoliv hodnotu tak dostanu vždy kladný výraz
Jinak samozřejmě že 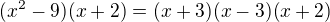
Vzít nulové body, a prozkoumat, kde to bude záporné, kde kladné a je to
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#6 02. 03. 2013 17:01 — Editoval ((:-)) (02. 03. 2013 17:21)
Re: racionální nerovnice s jednou neznámou
Offline
#7 02. 03. 2013 17:05 — Editoval Martin95k (02. 03. 2013 17:08)
Re: racionální nerovnice s jednou neznámou
Nakonec bychom přišli k tomu samému jako Freedy. Při zjišťování nulových bodů bychom zjistili, že čitatel žádné nemá (záporný D) a tedy neprotíná osu x, protože fce 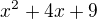 značí, že fce je konvexní a posunutá o 9 kladným směrem na ose y. Nebo ne?
značí, že fce je konvexní a posunutá o 9 kladným směrem na ose y. Nebo ne?
Offline
#8 02. 03. 2013 17:07 — Editoval teolog (02. 03. 2013 17:08)
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: racionální nerovnice s jednou neznámou
↑ Freedy:
Vaší reakci nechápu, nejprve píšete, že není potřeba nic rozkládat na součin a pak to sám rozložíte na součin.
Zkušenější student jako Vy samozřejmě na první pohled vidí, že čitatel je vždy kladný a že 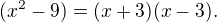 Nicméně se mi zdá lepší spíše předpokládat, že tazatel není tak zkušený a potřebuje detailnější popis, než to odbýt a tazatelovi nebude jasné nic a bude se znovu ptát.
Nicméně se mi zdá lepší spíše předpokládat, že tazatel není tak zkušený a potřebuje detailnější popis, než to odbýt a tazatelovi nebude jasné nic a bude se znovu ptát.
A to nemluvím ani o případech, kdy stejný příklad jen s jinými hodnotami může být mnohem komplikovanější a ani Vy na první pohled neuvidíte řešení či nulové body. A s tím se snažím pracovat, aby tazatel s mou radou dokázal případně vyřešit i složitější příklady.
Offline
#9 02. 03. 2013 17:09 — Editoval ((:-)) (02. 03. 2013 17:21)
Re: racionální nerovnice s jednou neznámou
Offline
#10 02. 03. 2013 17:14 — Editoval Freedy (02. 03. 2013 17:15)
Re: racionální nerovnice s jednou neznámou
:D dobrá dobrá, už mě nechte. Doufám že elisa to pochopila.
To rozkládat sem myslel roznásobovat původně -.- zaměnil jsem si to s jiným pojmem.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » racionální nerovnice s jednou neznámou (TOTO TÉMA JE VYŘEŠENÉ)