Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 03. 2013 21:31 — Editoval DUMAG (19. 03. 2013 22:05)
Príklady z kombinatoriky
Šikovnejší prosím pomôžte:
1. Do šachového klubu chodí 6 chlapcov a 4 dievčatá.Koľkýmispôsobmi z nich možno vybrať trojicu ak medzi vybranými má byť aspoň jedno dievča a aspoň jeden chlapec?
2. Koľkými spôsobmi si môžu tri deti rozdeliť 5 malých a 6 veľkých zošitov?
3. Koľkými spôsobmi možno prečítať MATEMATIKA
MATEMATIKA
ATEMATIKA
TEMATIKA
EMATIKA
MATIKA
ATIKA
TIKA
IKA
KA
A
4. Vypočítajte : 
Šikuľkám a šikuľkom ďakujem
Offline
- (téma jako vyřešené označil(a) DUMAG)
#2 19. 03. 2013 22:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Príklady z kombinatoriky
Zdravím Vás,
dostudujte, prosím, pravidla 2, 3. Nebo téma budu zamykat. Děkuji za pochopení.
Offline
#4 20. 03. 2013 00:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Príklady z kombinatoriky
↑ zdenek1:
:-) a co ta 3. úloha? Kolegovi se ztratilo ze zadání slovo "na obrázku". Má být: "Koľkými spôsobmi na obrázku možno prečítať MATEMATIKA". A obrázek je to, co má pod textem, má být lépe uspořadan, aby bylo vidět možné směry čtení.
Jinak kolegovi jsem pravidla četla zde. A také kolega si má udělat jasno, zda píše v rodu mužském a tomu přizpůsobí značku u jména, nebo jak :-) Také nahlašuji, že autička jsem poklidila (snad :-)
Zdravím.
Offline
#5 20. 03. 2013 06:38
Re: Príklady z kombinatoriky
↑ jelena:
zdenek 1 -ďakujem za pomoc.
Jelena - pravidla som si už prečítal,budem sa nimi riadiť .Myslím si však,že keď to neviem riešiť-prosím o pomoc, tak neviem ake riešenie napíšem,ale v poriadku-máte také pravidlá a ja ako vidím mám len dve možnosti -nepísať riešenie a budem zamknutý,alebo písať,keď aj blbosti a nebudem zamknutý.Zrejme si si inač všimla,že nechcem riešenie príkladov,aby to nedajbože niekto za mňa vypočítal-viď Arabela ale len vzorce.
Aj tak Ti ďakujem, lebo vidím,že v matike sa vyznáš.
Offline
#7 20. 03. 2013 09:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Príklady z kombinatoriky
↑ zdenek1:
děkuji, výsledek jsem viděla v odkazu s kompletním textem (i princip úlohy popsat dokáži), bohužel výsledek z hlavy nevytvořím.
↑ DUMAG:
ano, rozumím. V pravidlech, co se odkazuji, jsou 2 momenty:
a) dávat jednu úlohu do tématu se hodí pro přehlednost,
b) psát nástin vlastního postupu (úvah apod.) se hodí pro cílené nasměrování.
Důkazy obou přístupu jste viděl ve Vašem předchozím tématu. Doporučuji zanalyzovat.
Mně je to v principu jedno, určitě zmatek zvládám, jen si myslím, že Moderátor je od toho, aby:
a) uživatelům napomohl k pohodlnějšímu působení na fóru,
b) podpořil dosud platná pravidla, nebo přispěl k zahájení debaty nad novelou, pokud to prospěji k bodu a).
Vyžívat se v zavírání témat nijak nepotřebuji, i když ono to tak občas působí :-).
lebo vidím,že v matike sa vyznáš.
:-) ne, ne - jsem jen přesvědčivý důkaz tvrzení mé maminky, že "I králíka jde naučit hrát na buben" (ještě trošku tuto dovednost musím udržovat, než dovedu milého syna na strojní fakultu, představa, že mi ještě vrazí dohled na výukou vnoučat, je zatím dost mlhavá :-)
nechcem riešenie príkladov,aby to nedajbože niekto za mňa vypočítal-viď Arabela ale len vzorce.
Kdyby v kombinatorice šlo jen o vzorce, tak jsem mistr v oboru. Bohužel, jde pravě o uvažování, na které nemám.
Zdar v počítání přeji a dodržujte pravidla (nebo navrhujte nová :-).
Offline





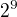 pokud to čtení musí "navazovat"
pokud to čtení musí "navazovat"