Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Podílové kritérium (TOTO TÉMA JE VYŘEŠENÉ)
#1 22. 03. 2013 18:17 — Editoval Polopat (22. 03. 2013 18:18)
Podílové kritérium
Zdravím,
není mi jasná jedna věc na podílovém kritériu, byl bych vděčný za "nakopnutí". Znění kritéria je:
Při podílovém (d'Alembertově) kritériu konverguje řada s kladnými členy 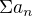 tehdy, existuje-li reálné číslo
tehdy, existuje-li reálné číslo  takové, že pro každé
takové, že pro každé  platí
platí 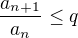 . Pokud je
. Pokud je 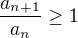 , pak řada diverguje.
, pak řada diverguje.
Proč je v kritériu v první části nutná existence  a nejde prostě jenom napsat "když je
a nejde prostě jenom napsat "když je  "? A naopak proč to v druhé části kritéria lze?
"? A naopak proč to v druhé části kritéria lze?
Offline
- (téma jako vyřešené označil(a) Polopat)
#2 22. 03. 2013 22:17 — Editoval martisek (22. 03. 2013 22:18)
Re: Podílové kritérium
↑ Polopat: nestačí. Například pro harmonickou řadu
nestačí. Například pro harmonickou řadu 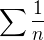 je
je 
a řada přesto diverguje.
Ve druhém případě 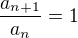 svědčí zcela jasně o divergenci, protože to znamená že
svědčí zcela jasně o divergenci, protože to znamená že 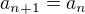 a
a 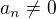 (jinak by nebyl definován zlomek). To znamená, že nemůže platit lim a_n = 0 a není splněna nutná podmínka konvergence.
(jinak by nebyl definován zlomek). To znamená, že nemůže platit lim a_n = 0 a není splněna nutná podmínka konvergence.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#3 23. 03. 2013 09:06
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Podílové kritérium (TOTO TÉMA JE VYŘEŠENÉ)
